On this page you can find interactive environments, games and problems for Secondary learners.
Interactive environments
These general interactive environments can be used to support learners' work on a variety of activities.
-
 interactivityFavourite
interactivityFavouriteDice and spinners interactive
Simple dice and spinners tool for experiments.
-
 interactivityFavourite
interactivityFavouriteCuisenaire environment
An environment which simulates working with Cuisenaire rods.
-
 interactivityFavourite
interactivityFavouriteDominoes environment
These interactive dominoes can be dragged around the screen.
-
 interactivityFavourite
interactivityFavouriteVirtual geoboard
This virtual geoboard allows you to create shapes by stretching rubber bands between pegs on the board.
-
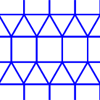 interactivityFavourite
interactivityFavouriteTessellation interactivity
An environment that enables you to investigate tessellations of regular polygons
Interactive activities
These problems and games all have interactive content, making them ideal for students to tackle on tablets or laptops.
-
-
 gameFavourite
gameFavouriteThe remainders game
Play this game and see if you can figure out the computer's chosen number.
-
-

-
 problem
problemMatching fractions, decimals and percentages
Can you match pairs of fractions, decimals and percentages, and beat your previous scores?
-
 problem
problemGot it
A game for two people, or play online. Given a target number, say 23, and a range of numbers to choose from, say 1-4, players take it in turns to add to the running total to hit their target.
-
 problem
problemYour number is...
Think of a number and follow the machine's instructions... I know what your number is! Can you explain how I know?
-
 problem
problemTreasure hunt
Can you find a reliable strategy for choosing coordinates that will locate the treasure in the minimum number of guesses?
-
 problem
problemMissing multipliers
What is the smallest number of answers you need to reveal in order to work out the missing headers?
-
 problem
problemThe Number Jumbler
The Number Jumbler can always work out your chosen symbol. Can you work out how?
-

-
 problem
problemMore less is more
In each of these games, you will need a little bit of luck and your knowledge of place value to develop a winning strategy.
-
 problem
problemFactor lines
Arrange the four number cards on the grid, according to the rules, to make a diagonal, vertical or horizontal line.
-
 problem
problemRemainders
I'm thinking of a number. My number is both a multiple of 5 and a multiple of 6. What could my number be?
-
 problem
problemNumber lines in disguise
Some of the numbers have fallen off Becky's number line. Can you figure out what they were?
-
 gameFavourite
gameFavouriteFactors and multiples game
A game in which players take it in turns to choose a number. Can you block your opponent?
-
 problem
problemFruity totals
In this interactivity each fruit has a hidden value. Can you deduce what each one is worth?
-

-

-
 problem
problemFrogs
How many moves does it take to swap over some red and blue frogs? Do you have a method?
-
 problem
problemPicturing triangular numbers
What do you notice about the sum of two identical triangular numbers?
-
 problem
problemNumber pyramids
Try entering different sets of numbers in the number pyramids. How does the total at the top change?
-
 problem
problemTilted squares
It's easy to work out the areas of most squares that we meet, but what if they were tilted?
-
 problem
problemIsosceles triangles
Draw some isosceles triangles with an area of $9$cm$^2$ and a vertex at (20,20). If all the vertices must have whole number coordinates, how many is it possible to draw?
-
 problem
problemPartitioning revisited
We can show that (x + 1)² = x² + 2x + 1 by considering the area of an (x + 1) by (x + 1) square. Show in a similar way that (x + 2)² = x² + 4x + 4
-
 problem
problemTriangles in circles
Can you find triangles on a 9-point circle? Can you work out their angles?
-
 problem
problemFlippin' discs
Discs are flipped in the air. You win if all the faces show the same colour. What is the probability of winning?
-

-
 problem
problemHow far does it move?
Experiment with the interactivity of "rolling" regular polygons, and explore how the different positions of the dot affects the distance it travels at each stage.
-
 problem
problemSubstitution cipher
Find the frequency distribution for ordinary English, and use it to help you crack the code.
-
 problem
problemIn the bag
Can you guess the colours of the 10 marbles in the bag? Can you develop an effective strategy for reaching 1000 points in the least number of rounds?
-
 problem
problemInteractive spinners
This interactivity invites you to make conjectures and explore probabilities of outcomes related to two independent events.
-
 problem
problemReaction timer
This problem offers you two ways to test reactions - use them to investigate your ideas about speeds of reaction.
-
 problem
problemShifting times tables
Can you find a way to identify times tables after they have been shifted up or down?
-

-
 problem
problemYour number was...
Think of a number and follow my instructions. Tell me your answer, and I'll tell you what you started with! Can you explain how I know?
-
 problem
problemRolling around
A circle rolls around the outside edge of a square so that its circumference always touches the edge of the square. Can you describe the locus of the centre of the circle?
-
 problem
problemMore number pyramids
When number pyramids have a sequence on the bottom layer, some interesting patterns emerge...
-
 problem
problemSquare coordinates
A tilted square is a square with no horizontal sides. Can you devise a general instruction for the construction of a square when you are given just one of its sides?
