Square coordinates
A tilted square is a square with no horizontal sides. Can you devise a general instruction for the construction of a square when you are given just one of its sides?
Problem
Square Coordinates printable sheet
Play with this interactivity until you can draw tilted squares confidently.
Formulate and describe a general instruction for the construction of a square when you are given two adjacent corners.
Formulate and describe a general instruction for the construction of a square when you are given two opposite corners.
Decide whether any of the collections of points below form a square.
If so, which ones?
Can you do this without plotting the points on a grid?
1. $(8,3)$, $(7,8)$, $(2,7)$, $(3,2)$
2. $(3,3)$, $(7,4)$, $(8,8)$, $(4,7)$
3. $(16,19)$, $(18,22)$, $(21,20)$, $(19,17)$
4. $(4,20)$, $(21,19)$, $(20,2)$, $(3,3)$
Explain how you decided.
You may now enjoy playing Square It.
Getting Started
You might like to play Square It before working on this problem.
Can you describe how many steps left/right and how many steps up/down you need to take to go from one corner of a square to the next? And to the next?
Student Solutions
Hannah tackled the first part of this problem. Here are the squares she drew:
(a)
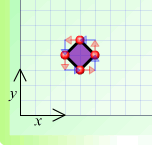
(b)
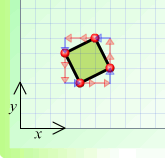
(c)
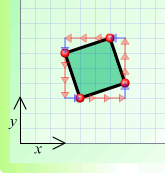
(d)
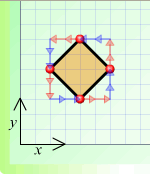
(e)
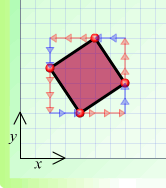
In all of these, the side AB could either be from the bottom corner to the right, or from the left corner to the top. Do you see why?
Hannah went on to complete the arrow notation for these squares. She's taken the side AB to be from the bottom up to the right.
(a) $A \: 1 \rightarrow +1 \uparrow B \: 1 \leftarrow + 1 \uparrow C \:1 \leftarrow + 1 \downarrow D \:1 \rightarrow + 1 \downarrow A$
(b) $A \: 2 \rightarrow + 1 \uparrow B \: 1 \leftarrow + 2 \uparrow C \: 2 \leftarrow + 1 \downarrow D \: 1 \rightarrow + 2 \downarrow A$
(c) $A \: 3 \rightarrow + 1 \uparrow B \: 1 \leftarrow + 3 \uparrow C \: 3 \leftarrow + 1 \downarrow D \: 1 \rightarrow + 3 \downarrow A$
(d) $A \: 2 \rightarrow + 2 \uparrow B \: 2 \leftarrow + 2 \uparrow C \: 2 \leftarrow + 2 \downarrow D \: 2 \rightarrow + 2 \downarrow A$
(e) $A \: 3 \rightarrow + 2 \uparrow B \: 2 \leftarrow + 3 \uparrow C \: 3 \leftarrow + 2 \downarrow D \: 2 \rightarrow + 3 \downarrow A$
Suppose you're given the side $A \: a \rightarrow + b \: \uparrow B$. (I noticed that $\downarrow$ could be written as $-\uparrow$ and $\leftarrow$ could be written as $-\rightarrow$, so $a$ and $b$ could be negative, but that doesn't matter. This makes it a bit easier, as we only have two sorts of arrow then.) Then the square is either $$A \: a \rightarrow + b \uparrow B \: -b \rightarrow +a \uparrow C \: -a \rightarrow -b \uparrow D \: b \rightarrow -a \uparrow A$$ or $$A \: a \rightarrow + b \uparrow B \: b \rightarrow -a \uparrow C \: -a \rightarrow - b \uparrow D \: -b \rightarrow + a \uparrow A.$$
- (8,3), (7,8), (2,7), (3,2). In arrow notation, this would be $A \: -1 \rightarrow +5 \uparrow B \: -5 \rightarrow - 1 \uparrow C \: 1 \rightarrow - 5 \uparrow D \: 5 \rightarrow + 1 \uparrow A$. This is of the first form, with $a=-1$ and $b=5$. So this is a square.
- (3,3), (7,4), (8,8), (4,7). In arrow notation, this would be $A \: 4 \rightarrow + 1 \uparrow B \: 1 \rightarrow + 4 \uparrow C \: -4 \rightarrow - 1 \uparrow D \: -1 \rightarrow - 4 \uparrow D$. This isn't of either form, so the points don't form a square.
- (16,19), (18,22), (21,20), (19,17). In arrow notation, this would be $A \: 2 \rightarrow + 3 \uparrow B \: 3 \rightarrow - 2 \uparrow C \: -2 \rightarrow - 3 \uparrow D \: -3 \rightarrow + 2 \uparrow A$. This is of the second form, with $a=2$ and $b=3$, so the points form a square.
- (4,20), (21,19), (20,2), (3,3). In arrow notation, this would be $A \: 17 \rightarrow - 1 \uparrow B \: -1 \rightarrow - 17 \uparrow C \: -17 \rightarrow + 1\uparrow D \: 1 \rightarrow + 17\uparrow A$. This is also of the second form, with $a=17$ and $b=-1$, so the points form a square.
Teachers' Resources
Why do this problem?
This problem emphasises to students that squares don't just exist in their usual orientation. It goes well with the game Square It
Possible approach
Display the interactivity. Ask for volunteers to move the corners to make a different square.
Fix a couple of corners and challenge students to complete the square.
Set students to work in pairs (ideally at computers) practising making squares until they can answer the key questions below. Suggest they make a variety of squares of different sizes and note down the sets of coordinates of their completed squares.
This could lead to a plenary discussion or, when appropriate, challenge students to work away from the computer on the final questions in the problem. This sheet provides further practice with tilted squares, but without reference to their co-ordinates.
Key questions
Possible extension
Possible support
Students can answer the last four questions by plotting the points provided and boxing them in to decide whether they make a square.
