Developing mathematical thinking - working systematically
Working Systematically is part of our Developing Mathematical Thinking Primary and Secondary collections.
This page for teachers accompanies the Working Systematically Primary and Secondary resources.
You may wish to watch the recording of the webinars, which draw on the resources below to discuss how teachers can offer students opportunities to work systematically, and to appreciate the value of this approach.
During this webinar, we had a go at the following tasks:
Number Jumbler
Button-up Some More
TWO and TWO
During this webinar, we had a go at the following tasks:
Number Jumbler
M, M and M
Charlie's Delightful Machine
Pick's Theorem
The mathematical world is an ordered world, so mathematicians work in a structured way and often look for patterns. Working in a systematic way allows mathematicians to reveal underlying structures, and make sense of what initially may seem messy and chaotic.
There are many different ways of working systematically, and the context might determine the most appropriate strategy to adopt in each case. Below are examples of working systematically in a variety of different contexts.
We are often frustrated when students do not work systematically, but do they really know what we mean when we challenge them to work systematically? We hope that the examples below model a variety of approaches, which could be discussed with students, and may help them appreciate the value of working in this way. Students could then build on these approaches when given the opportunity to work on the problems listed in the Primary and Secondary collections. All the problems have Teachers' Resources, which draw attention to the value of approaching each task in a systematic way.
Making small adjustments, when going from the particular to the general - Number Jumbler
After everyone has had a go, they are likely to be very surprised that the interactivity was able to predict the image they were looking at. So how could they explain this...?
Students might want to try to some further examples, so a good strategy might be for each new example to have a starting number that differs by just one from the previous starting number, and to see what happens.
For example, if their initial first number was 34, their result would be 27.
Next, they could try 33 and 35, both of which give 27 again!
Then, they could try 32 and 36, both of which give 27 again...
If someone started with 50, their result would be 45.
If they start with 51, 52, 53... their result would still be 45...
If they start with 49, 48, 47... their result would be 36...
This then leads to Conjecturing and Generalising (Primary and Secondary)
See also:
Reach 100 (Age 7-11)
Add to 200 (Age 11-14)
Reflecting Squarely (Age 11-14), in particular Andrei's solution
Which is Cheaper? (Age 14-16)
Listing in an ordered way - Button-up Some More
A possible starting point is to try a simpler case with three buttons: Top, Middle and Bottom
Starting with the top button:
T M B
T B M
Starting with the middle button:
M T B
M B T
Starting with the bottom button:
B T M
B M T
So there are six ways of buttoning up three buttons
Working on three buttons may give students the confidence to tackle four buttons in a similar way
With four buttons, we can keep track of what we're doing more easily by using numbers 1, 2, 3, 4 to represent the buttons
Starting with button number 1:
1 2 3 4
1 2 4 3
1 3 2 4
1 3 4 2
1 4 2 3
1 4 3 2
Starting with button number 2:
2 1 3 4
2 1 4 3
2 3 1 4
2 3 4 1
2 4 1 3
2 4 3 1
Can you find the six ways starting with button number 3?
Can you find the six ways starting with button number 4?
So there are 24 ways of buttoning up four buttons
Mathematicians like saving themselves some time, so could we have built on the three-button results and saved ourselves having to list all the possibilities?
We know that three buttons can be done up in six different ways.
If we have a fourth button, it can be done up first, second, third or fourth. We know that in each case, the other three buttons can be done up in six different ways, giving us 6 x 4 possible orders for four buttons:
| _ T M B _ T B M _ M T B _ M B T _ B T M _ B M T |
T _ M B T _ B M M _ T B M _ B T B _ T M B _ M T |
T M _ B T B _ M M T _ B M B _ T B T _ M B M _ T |
T M B _ T B M _ M T B _ M B T _ B T M _ B M T _ |
See also:
Robot Monsters (Age 5-7)
Tangram Tangle (Age 5-11)
School Fair Necklaces (Age 5-11)
Making Cuboids (Age 7-11)
Consecutive Numbers (Age 7-14)
Squares in Rectangles (Age 11-14)
1 Step 2 Step (Age 11-14)
Breaking down a problem and tackling each part separately - Two and Two
- We could focus on the possible values of the letter T:
$\quad \text{T}\hspace{1mm} \text{W}\hspace{1mm} \text{O}$
$\underline{+\, \text{T}\hspace{1mm} \text{W}\hspace{1mm} \text{O}}$
$\underline{\, \, \, \text{F}\hspace{1mm} \text{O}\hspace{1mm} \text{U}\hspace{1mm} \text{R}}$
T $\geq$ 5 and F = 1
Therefore T = 5, 6, 7, 8 or 9
If T = 5:
|
$\quad \text{5}\hspace{1mm} \text{_}\hspace{1mm} \text{_}$ |
or |
$\quad \text{5}\hspace{1mm} \text{_}\hspace{1mm} \text{_}$ |
In the example on the left, if letter O equals 0, R would also be 0 (looking at the ones column), which is not allowed
In the example on the right, both F and O cannot be equal to 1
Therefore T $\neq$ 5
If T=6, can you convince yourself that there are no solutions?
If T=7:
|
$\quad \text{7}\hspace{1mm} \text{_}\hspace{1mm} \text{_}$ |
or |
$\quad \text{7}\hspace{1mm} \text{_}\hspace{1mm} \text{_}$ |
If letter O = 4:
| $\quad \text{7}\hspace{1mm} \text{_}\hspace{1mm} \text{4}$ $\underline{+\, \text{7}\hspace{1mm} \text{_}\hspace{1mm} \text{4}}$ $\underline{\, \, \, \text{1}\hspace{1mm} \text{4}\hspace{1mm} \text{_}\hspace{1mm} \text{8}}$ |
Therefore W $< $ 5 W cannot be 0, 1, 2 or 4 Therefore only one solution when W=3 |
|
| $\quad \text{7}\hspace{1mm} \text{3}\hspace{1mm} \text{4}$ $\underline{+\, \text{7}\hspace{1mm} \text{3}\hspace{1mm} \text{4}}$ $\underline{\, \, \, \text{1}\hspace{1mm} \text{4}\hspace{1mm} \text{6}\hspace{1mm} \text{8}}$ |
If letter O = 5:
| $\quad \text{7}\hspace{1mm} \text{_}\hspace{1mm} \text{5}$ $\underline{+\, \text{7}\hspace{1mm} \text{_}\hspace{1mm} \text{5}}$ $\underline{\, \, \, \text{1}\hspace{1mm} \text{5}\hspace{1mm} \text{_}\hspace{1mm} \text{0}}$ |
Therefore W $\geq$ 5 W cannot be 5, 7, 8, or 9 Therefore only one solution when W=6 |
|
| $\quad \text{7}\hspace{1mm} \text{6}\hspace{1mm} \text{5}$ $\underline{+\, \text{7}\hspace{1mm} \text{6}\hspace{1mm} \text{5}}$ $\underline{\, \, \, \text{1}\hspace{1mm} \text{5}\hspace{1mm} \text{3}\hspace{1mm} \text{0}}$ |
Using similar reasoning, can you convince yourself that when T = 8, there are three solutions and when T = 9 there are two solutions?
- Alternatively, we could focus on the possible values of the letter O:
$\quad \text{T}\hspace{1mm} \text{W}\hspace{1mm} \text{O}$
$\underline{+\, \text{T}\hspace{1mm} \text{W}\hspace{1mm} \text{O}}$
$\underline{\, \, \, \text{F}\hspace{1mm} \text{O}\hspace{1mm} \text{U}\hspace{1mm} \text{R}}$
T $\geq$ 5 and F = 1
If we start with letter O, we will assume that it could be equal to 0, 1, 2, 3, 4, 5, 6, 7, 8 or 9
Letter O $\neq$ 0 because of R
Letter O $\neq$ 1 because of F
If letter O = 2:
| $\quad \text{_}\hspace{1mm} \text{_}\hspace{1mm} \text{2}$ $\underline{+\, \text{_}\hspace{1mm} \text{_}\hspace{1mm} \text{2}}$ $\underline{\, \, \, \text{1}\hspace{1mm} \text{2}\hspace{1mm} \text{_}\hspace{1mm} \text{4}}$ |
Therefore T = 6 |
| $\quad \text{6}\hspace{1mm} \text{_}\hspace{1mm} \text{2}$ $\underline{+\, \text{6}\hspace{1mm} \text{_}\hspace{1mm} \text{2}}$ $\underline{\, \, \, \text{1}\hspace{1mm} \text{2}\hspace{1mm} \text{_}\hspace{1mm} \text{4}}$ |
Therefore W < 5 No possible solutions for W Therefore letter O $\neq$ 2 |
If letter O = 3:
| $\quad \text{6}\hspace{1mm} \text{_}\hspace{1mm} \text{3}$ $\underline{+\, \text{6}\hspace{1mm} \text{_}\hspace{1mm} \text{3}}$ $\underline{\, \, \, \text{1}\hspace{1mm} \text{3}\hspace{1mm} \text{_}\hspace{1mm} \text{6}}$ |
Therefore T = 6, which is not allowed because T $\neq$ R Therefore letter O $\neq$ 3 |
If letter O = 4:
| $\quad \text{_}\hspace{1mm} \text{_}\hspace{1mm} \text{4}$ $\underline{+\, \text{_}\hspace{1mm} \text{_}\hspace{1mm} \text{4}}$ $\underline{\, \, \, \text{1}\hspace{1mm} \text{4}\hspace{1mm} \text{_}\hspace{1mm} \text{8}}$ |
Therefore, T = 7 |
| $\quad \text{7}\hspace{1mm} \text{_}\hspace{1mm} \text{4}$ $\underline{+\, \text{7}\hspace{1mm} \text{_}\hspace{1mm} \text{4}}$ $\underline{\, \, \, \text{1}\hspace{1mm} \text{4}\hspace{1mm} \text{_}\hspace{1mm} \text{8}}$ |
Therefore, W < 5 W cannot be 0, 1, 2, 4 |
Therefore, only one solution when W = 3
$\quad \text{7}\hspace{1mm} \text{3}\hspace{1mm} \text{4}$
$\underline{+\, \text{7}\hspace{1mm} \text{3}\hspace{1mm} \text{4}}$
$\underline{\, \, \, \text{1}\hspace{1mm} \text{4}\hspace{1mm} \text{6}\hspace{1mm} \text{8}}$
If letter O = 5:
| $\quad \text{_}\hspace{1mm} \text{_}\hspace{1mm} \text{5}$ $\underline{+\, \text{_}\hspace{1mm} \text{_}\hspace{1mm} \text{5}}$ $\underline{\, \, \, \text{1}\hspace{1mm} \text{5}\hspace{1mm} \text{_}\hspace{1mm} \text{0}}$ |
Therefore, T = 7 |
| $\quad \text{7}\hspace{1mm} \text{_}\hspace{1mm} \text{5}$ $\underline{+\, \text{7}\hspace{1mm} \text{_}\hspace{1mm} \text{5}}$ $\underline{\, \, \, \text{1}\hspace{1mm} \text{5}\hspace{1mm} \text{_}\hspace{1mm} \text{0}}$ |
Therefore, W $\geq$ 5 W cannot be 5, 7, 8 or 9 |
Therefore, only one solution when W = 6
$\quad \text{7}\hspace{1mm} \text{6}\hspace{1mm} \text{5}$
$\underline{+\, \text{7}\hspace{1mm} \text{6}\hspace{1mm} \text{5}}$
$\underline{\, \, \, \text{1}\hspace{1mm} \text{5}\hspace{1mm} \text{3}\hspace{1mm} \text{0}}$
Convince yourself that:
- For letter O = 6 there are two solutions
- For letter O = 7 there is one solution
- For letter O = 8 there are two solutions
- For letter O = 9 there are no solutions
See also:
Factor Lines (Age 7-11)
Summing Consecutive Numbers (Age 11-14)
What's Possible? (Age 14-16)
Combining the previous two strategies - M, M and M
Mean = 4
Median = 3
Mode = 3
Therefore:
Total of the five numbers must be 20
Middle number must be 3 when lined up in numerical order
There must be at least two 3s
- We could focus on the possible positions of the 3s:
If the two 3s are in positions two and three:
_ 3 3 _ _
1 3 3 4 9
1 3 3 5 8
1 3 3 6 7
2 3 3 4 8
2 3 3 5 7
If the two 3s are in positions three and four:
_ _ 3 3 _
1 2 3 3 11
If the three 3s are in positions one, two and three:
3 3 3 _ _
3 3 3 4 7
3 3 3 5 6
If the three 3s are in positions two, three and four:
_ 3 3 3 _
1 3 3 3 10
2 3 3 3 9
If the three 3s are in positions three, four and five:
_ _ 3 3 3
Impossible
Convince yourself that:
- there is only one solution with four 3s
- there are no solutions with five 3s
- Alternatively, we could focus on the possible starting numbers:
Starting with a 1:
1 _ 3 _ _
1 2 3 3 11
1 3 3 3 10
1 3 3 4 9
1 3 3 5 8
1 3 3 6 7
Starting with a 2:
2 _ 3 _ _
2 3 3 3 9
2 3 3 4 8
2 3 3 5 7
Can you convince yourself that there are three solutions starting with a 3?
See also:
Symmetry Challenge (Age 7-11)
American Billions (Age 11-14), and in particular Ali's solution
Isosceles Triangles (Age 11-14)
Cuboids (Age 11-14)
Using recording to capture results in a structured way - Charlie's Delighful Machine
After everyone has entered a few numbers to see what happens, students may be challenged to find if it is possible to light all the light bulbs at the same time...
If approached randomly, it would be very difficult to answer the question.
However, if a table is created, like the one below, it will be much easier to identify which numbers light up each colour.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | |
| Yellow | X | X | X | ||||||||||||||||||
| Red | X | X | X | X | X | X | X | ||||||||||||||
| Green | X | X | X | X | X | X | X | ||||||||||||||
| Blue | X | X |
When do yellow and red light up together?
When do yellow and green light up together?
When do yellow and blue light up together? ...
This can then lead to Conjecturing and Generalising (Primary and Secondary)
See also:
Light the Lights Again (7-11)
Fifteen Cards (Age 7-11)
Add to 200 (Age 11-14)
Summing Consecutive Numbers (Age 11-14)
American Billions (Age 11-14), and in particular Ali's solution
What's Possible? (Age 14-16)
Which is Cheaper? (Age 14-16)
Changing one variable at a time to reveal structure (going from the particular to the general) - Pick's Theorem
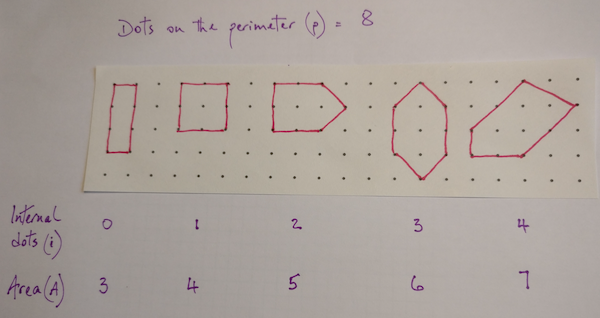
The challenge is to find a relationship between the number of dots on the perimeter (p), the number of internal dots (i) and the area (A) of any shape with vertices on the dots of a square grid.
- We could fix p, and see how the area changes as i changes:
If we fix the number of dots on the perimeter at 8:
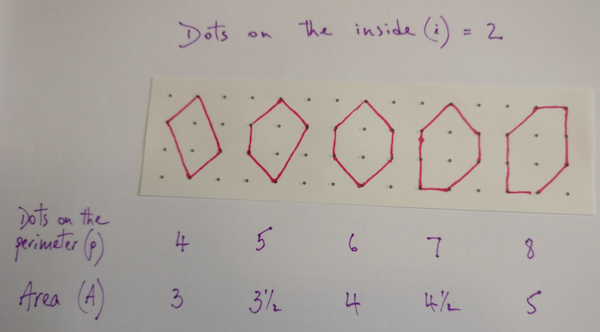
- Alternatively, we could fix i, and see how the area changes as p changes:
- Alternatively, we could fix the area (try for example A=6). What happens to the value of P as i increases from 0 to 1 to 2...?
This can then lead to Conjecturing and Generalising.
See also:
Add to 200 (Age 11-14)
Tilted Squares (Age 11-14) and the accompanying Teachers' Resources, which contain a video of this problem being used in the classroom
Further reading:
Thinking Mathematically by John Mason, Leone Burton and Kaye Stacey
Problem-Solving Strategies In Mathematics: From Common Approaches To Exemplary Strategies by Alfred
S Posamentier and Stephen Krulik
- Log in to post comments