Reflecting squarely
In how many ways can you fit all three pieces together to make shapes with line symmetry?
Problem
Reflecting Squarely printable sheet
Reflecting Squarely printable grids
The three pieces below can be fitted together to make shapes with at least one line of symmetry.

The vertices of each piece must lie on grid points, and you must not overlap two pieces.

The pieces must be placed edge to edge, so this is not allowed.

This arrangement does not satisfy the criteria because the shape does not have a line of symmetry.
Can you find all the possible solutions? (There are more than six.)
How can you be sure you've found them all?
Here are some further questions to explore:
Design your own set of three shapes, with a total area of 10 square units, as above.
How many ways can they be arranged to make symmetrical shapes?
Can you find a set of three such shapes which can be arranged into more symmetrical shapes than those in the original problem?
Can you find three such shapes which can never be arranged to make a symmetrical shape?
You may wish to print copies of the shapes.
Here is an interactive you might like to use to try out your ideas. The red dot can be used to rotate the pieces and the blue dot can be used to move the pieces. To flip the pink piece, click on it.
This problem is based on one found in the Dime "Line Symmetry A" pack, produced by Tarquin Publications
Getting Started
Try using a mirror to check your symmetries.
Try keeping the biggest shape fixed in one position, place the rectangle systematically in all possible positions, and see whether the square can be added to make a symmetrical shape.
Student Solutions
An excellent solution from Andrei of School 205 Bucharest. I like this very much because of the effective and systematic approach he took to investigating the problem.
Here is Andrei's solution:
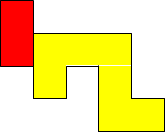
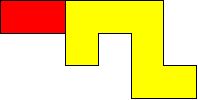
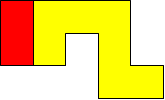
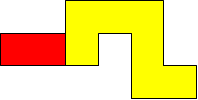
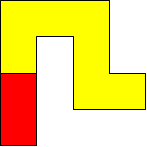
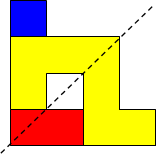
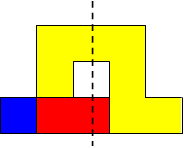
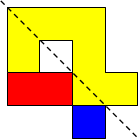
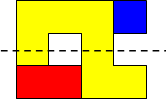
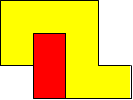
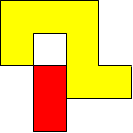
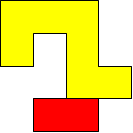
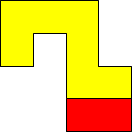
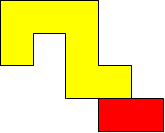
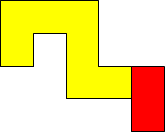
I worked systematically. I took the big (yellow) piece and I placed the rectangle in all the possible locations around it (both vertically and horizontally). Then I looked if the figure admitted a symmetry line (vertical, horizontal, or at a 45$^{\circ}$ angle) if I added a small square (blue). Here is all my work and the solutions I found, with the corresponding symmetry line:
Image
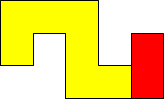
| Image
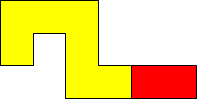
| Image

|
Image
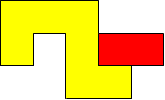
| Image

| Image
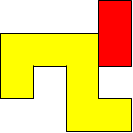
|
Image
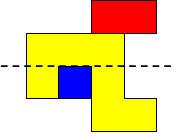
| Image
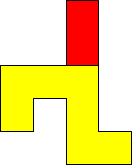
| Image

|
Image
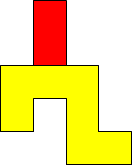
| Image

| Image
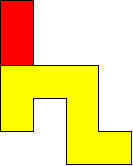
|
Image

| Image
| Image
|
Image
| Image
| Image
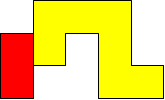
|
Image
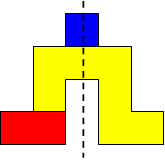
| Image
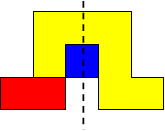
| Image
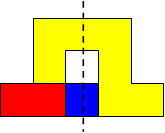
|
Image
| Image
| Image
|
Image
| Image
| Image
|
Image
| Image
| Image

|
Image
| Image

| Image
|
Image
|
Teachers' Resources
Why do this problem?
This problem makes students think about the symmetries of many different shapes. There will be opportunities for instant feedback, and a challenge that will engage the whole class in an activity that offers choice and room for creativity. The students have to take responsibility for checking each other's work, since the teacher clearly can't be expected to anticipate all the possible combinations that might be generated.
Possible approach
These printable resources may be useful: Reflecting Squarely (worksheet),
Reflecting Squarely Grids.
This problem could easily be used as it stands, as one of many activities on reflection symmetry. It can also be expanded, leading into a richer task:
As students enter, have copies of the three pieces available (on an OHP/blu-tacked to the board/on desks - card shapes or multilink (interlocking cubes)). Ask the class to find a few arrangements that are symmetrical. Keep a record of correct solutions as they are suggested.
Give students time to work individually/in pairs trying to find all the others. After a while students could be invited to draw new solutions on the board. Say that students have found only six arrangements, suggest that the set of three shapes is called a '6-ways-set'.
"Now it is time to 'beat the problem'. You can design your own three shapes, like the original, all made from squares on a square grid, with a total area of 10. Do you think we can find 3 shapes which can be put together symmetrically in more ways than the original problem? i.e. we're looking for a 7-ways-set, an 8-ways-set... (If anyone finds more symmetrical combinations for the original problem, then this task becomes even more challenging!)
"Between us, can we find a complete collection: a 0-ways-set, a 1-ways-set, a 2-ways-set... ?"
"When you have designed a set, and think you have found all the symmetrical arrangements, draw them clearly and stick your work to the board, for others to check." The board could be prepared with headings: 0-ways-sets, 1-ways-sets, 2-ways-sets... Ask all students to take responsibility for checking at least one displayed solution and confirm that it is in the right category.
Keep the work on display at the end of the lesson, so that students (from this class or another) can add to it over the next couple of weeks.
Key questions
Where can the mirror lines be?
Is there a systematic way of checking that you've found all the arrangements?
Possible support
Provide mirrors, and/or scissors so students can cut out their arrangement of shapes and fold them to check potential mirror lines.
Possible extension
Students might like to look at Andrei's solution and try to understand the logic behind his approach.
Encourage students to find three shapes that have very few possible arrangements (or none), and/or more than anything found so far.
