Pick's Theorem
Polygons drawn on square dotty paper have dots on their perimeter (p) and often internal (i) ones as well. Find a relationship between p, i and the area of the polygons.
Problem
Pick's Theorem printable worksheet
To work on this problem you may want to print out some dotty paper
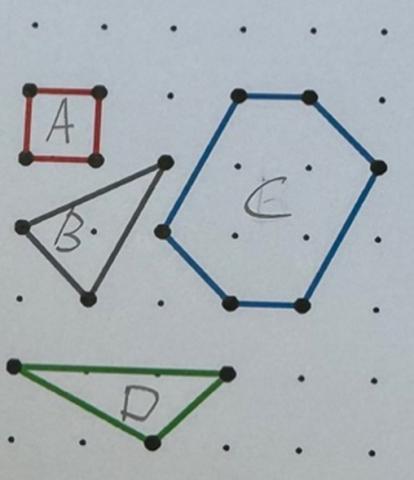
When the dots on square dotty paper are joined by straight lines the enclosed figures have dots on their perimeter ($p$) and often internal ($i$) ones as well.
Figures can be described in this way: $(p, i)$.
For example, the red square has a $(p,i)$ of $(4,0)$, the grey triangle $(3,1)$, the green triangle $(5,0)$ and the blue hexagon $(6,4)$:

Each figure you produce will always enclose an area ($A$) of the square dotty paper.
The examples in the diagram have areas of $1$, $1 {1 \over 2}$, and $6$ sq units.
Check that you agree.
Draw more figures and keep a record of their perimeter points ($p$), interior points ($i$) and areas ($A$).
Can you find a relationship between these three variables?
Can you find the area of any polygon once you know the number of perimeter points and interior points?
Click here for a poster of this problem.
Getting Started
* How many different figures can be described as $(4, 0)$?
* What do you notice about $(4,0)$ figures?
* Choose another particular value for $(p,i)$ and explore different shapes.
* Have you tried drawing shapes with the same area?
* What do you notice about those figures whose areas are the same?
* What ways are there of increasing the area by $1$ unit?
* Draw more figures; tabulate the information about their perimeter points ($p$), interior points ($i$) and their areas ($A$).
Student Solutions
Abheer, Anirved, Aslesha, Asma, Dia, Eshaan, Harshad, Harshika, Jaydeep, Nishika, and Siddhanth from Ganit Kreeda in India exaplined how to work out the areas of the shapes drawn on the dotty grids. Here is their work:

Jason from Stowe School in the UK, Lexie and Fiona and Diana from Dulwich College Beijing in China and the students from Ganit Kreeda used example shapes to build up, check and refine a formula for the area.
Lexie and Fiona described their process, including the shapes they drew. Click on the image to open a larger version:

I thought that if the area ($a$), $p$ and $i$ have a common relationship, then I should write an equation with the three variables in them. The equation I made was $a=p.i,$ but I needed to add different mathematical symbols and also numbers. After Lexie and I drew many different shapes (triangles, quadrilaterals, pentagons, hexagons and heptagons), we started to jot notes and thoughts down.
Eventually, our equation was $a=(p\div 2)+i-1.$
For example, a pentagon on a piece of dotted paper has this piece of information:
$p: 8$
$i: 5$
$a=?$
By knowing what $p$ and $i$ are equal to, we can use this to find out the area of this shape. First, substitute the information above into the equation Lexie and I found earlier, $a=(8\div2)+5-1.$ Then, solve it. The answer should be: $a=8.$
Diana and Jason thought about separating the effects of changing $p$ and $i.$ This is Diana's work:

The students from Ganit Kreeda drew lots of shapes and used a table to help them spot patterns and find a formula:

Shaunak from Ganit Mantahn in India made a video which shows the formula in action for a large shape. Click here to see Shaunak's video.
James from Norwich School in the UK, Yuning and Harris from Stowe School in the UK and Ci Hui from Queensland Academy of Science Mathematics and Technology in Australia worked on the problem in smaller chunks. They began by considering shapes with no internal points, one internal point, two internal points and so on. This is Harris's work:

Ci Hui, Yuning and James all found the same relationship, but wrote the formula so that $A$ was the subject. Ci Hui included a table to record and interpret the results. Below is Ci Hui's table and conculsion (click on the image to open a larger version), and click here to see Ci Hui's diagrams.

Aidan, Will, Bryan, Tony and Daniel from Dulwich College Beijing in China found the same formula using simultaneous equations:
Here is a list on the P and I and their area to find relations between them. (We are saying that the between each dot is 1.):

From the data above, we had assumed that the Pick’s Theorem is an equation, in form of "$A=aP+bI+c$", there, we got the following equations:
Equation 1: $4a+c=1$ (shape A)
Equation 2: $5a+c=1.5$ (shape D)
Subtracting equation 1 from 2, we get:
$a = 0.5$
Substituting the data from shape D into equation 2, we got $a=0.5, c=-1$
Now with $a$ and $c,$ we can easily work out that $b=1.$
With this we can work out that the equation
Which is $A=ap+bi+c=0.5p+i-1=\frac p 2 +i-1$
Having found the formula, Aidan, Will, Bryan, Tony, and Daniel decided to prove that it will always work. Their proof uses a related theorem, called Euler's Theorem, which is closely related to Pick's Theorem. Here is their proof (click on the image to open a larger version):
Now, after we had done trying to work out the theorem, we should start to [prove] the equation:

The students from Ganit Kreeda thought about shapes with the same area:

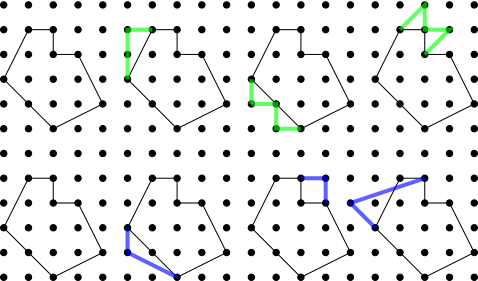
These ideas come directly from the formula. If you wanted to prove the formula, you could work backwards from these ideas. Look at these examples of removing one interior point and adding two perimeter points. Can you explain why the area is always the same?

The students from Ganit Kreeda also explored how you can increase the area by 1 unit:

These ideas come directly from the formula. If you wanted to prove the formula, you could work backwards from these ideas. Look at these examples of adding two perimeter points or one interior point. Does the area always increase by 1?
Teachers' Resources
Why do this problem?
At its simplest level this problem allows students to consolidate their understanding of how to calculate the area of irregular shapes. The extra mathematical demand comes from requiring students to identify the relationship between three variables.
Possible approach
This printable worksheet may be useful: Pick's Theorem.
You may be interested in our collection Dotty Grids - an Opportunity for Exploration, which offers a variety of starting points that can lead to geometric insights.
Draw a polygon on a square dotty grid on the board. Clarify that we shall be interested in three variables: the number of dots on the perimeter, $(p)$, the number of dots in the inside, $(i)$, and the area $(A)$. Ask students to work out the $(p)$, $(i)$ and $(A)$ of the shape that you have drawn.
Display the five shapes from the problem. For each, ask students to work in pairs and agree on the values of $(p)$, $(i)$ and $(A)$.
Draw attention to the two shapes that have an area of 1. What do they notice about their $(p)$ and $(i)$? Is this true for all shapes that have an area of 1? Allow the students some time to draw and share results. Confirm that there are an infinite number of possibilities of shapes which satisfy these conditions.
"The size of the shape will determine the area, so $(p)$ and $(i)$ may well determine the area. Your challenge is to draw some more shapes and find out if there is a relationship between these three variables."
Identify a central place where students can post their conjectures or other observations and encourage students to check their validity.
At an appropriate time bring the students back together to discuss the relationships they have discovered. Use this also as an opportunity to discuss effective strategies for identifying relationships, eg keeping one variable fixed.
You may wish to use the interactive pinboard, found here , to support your presentation/discussion of the problem.
Here is an account of one teacher's approach to using this problem.
Key questions
If $(p)$ is fixed and $(i)$ increases by 1, what is the effect on the area?
If $(i)$ is fixed and $(p)$ increases by 1, what is the effect on the area?
Possible support
Suggest that students start with shapes with small areas. How many different shapes can they draw for an area of 2? What possible values of $(p)$ and $(i)$ can they find? What about an area of 3..4..5...?
Possible extension
Does the same relationship hold when shapes are drawn on isometric dotty paper?
