This guidance is part of our Primary and Secondary 'Developing mathematical thinking' collections.
To complement this guidance, we hosted two teacher webinars. You may wish to watch the recording/s before or after taking a look at the guidance below.
Mathematicians are not only interested in answering questions, they also pose questions, make conjectures and test ideas.
Assuming students have been given the opportunity to explore a context, have noticed patterns and possible structures, and have worked systematically to generate more examples, they may then be in a position to conjecture, expressing ideas about what they think will happen more generally:
"I think ... will always happen."
"I think this method will always work."
"I think this is not just a special case."
"I think, if I change ...., then .... will happen."
Often, students go from question to question to question, rather than going from question to question to general. Moving from the particular to the general is a key mathematical process, and if we are to offer students opportunities to use specific examples as a springboard to generalising, then we may need to think about the following:
Values and ethos
- Mathematics is about relationships and interconnected ideas.
- Everyone can conjecture, everyone can work like a mathematician, everyone can contribute valuable ideas.
- A conjecturing atmosphere encourages students to feel comfortable about expressing their ideas.
- Being uncertain is not something to be embarrassed about ("I'd like to hear from those who are not quite sure..."); instead it provides a springboard for discussion. This is how we make progress.
Structural considerations
- “... everything that is said is treated as a conjecture that may require modifying" (John Mason).
- Tasks are chosen carefully so that they offer a window into a structure that can be used as a springboard to conjecturing and generalising.
- 'Making the private public': allowing space and time for students to share ideas, make, test and modify conjectures.
- 'Common boards' are used for displaying students' ideas and inviting responses (Alf Coles).
- A 'no hands up policy', where teachers select students randomly to contribute ideas, ensures all voices are heard (Dylan Wiliam).
Facilitating
“The aim is to reduce the pressure on ‘being correct’... when a learner offers a response to a question, try to catch yourself before you declare whether it is right or wrong; praise it as a conjecture, and invite others to consider whether they agree with it, or whether they would like to suggest a modification or a counter-example. In this way you can be responsible for the process of thinking, while the learners work together to decide correctness." (John Mason)
The teacher models the questions and comments a mathematician might make and, over time, encourages students to ask these questions themselves ('scaffolding and fading'):
- "Looking at these examples, what's the same? What's different?"
- "What do you think would happen if you changed ...?"
- "Do you think this will always happen?"
- "Does this example confirm your conjecture?"
- "Can you find a counter-example?"
- "What example might you try if you wanted to refute the conjecture?"
- "Can you think of an 'extreme' or 'nasty' example that would be worth testing?"
- "Do you agree with that conjecture? Why, or why not?"
- "How could you modify your conjecture?"
- "What do you think I'm going to ask you next?"
Below are tasks which aim to exemplify how students can move from the exploratory and working systematically phases, on to conjecturing and generalising.
Magic Vs
We're assuming students have found all the Magic Vs using the numbers 1-5. If you haven't had a go, you may like to try to do so now.
There are only three solutions:

Let's call the total of the three numbers in one arm the 'magic total'.
The magic totals of the Vs above are (from left to right) 8, 9 and 10.
This may lead to these initial conjectures about magic Vs:
I think...
- A magic V, using any five consecutive numbers, will always have an odd number at the bottom.
- I will always be able to find a magic V using any five consecutive numbers.
- If I use numbers 2-6, it won't be possible to make a magic V with an odd number at the bottom.
- If there are always three magic Vs with five consecutive numbers, there may always be five magic Vs with seven consecutive numbers.
- If we use numbers 2-6, the magic totals will be bigger than the magic totals using numbers 1-5.
- The magic totals of the magic Vs are always consecutive numbers.
Further testing may lead to these modified conjectures:
- If we use the numbers 3-7, 5-9, 7-11... (odd, even, odd, even, odd), the number at the bottom of the magic V will always be odd.
- If we use the numbers 2-6, 4-8, 6-10... (even, odd, even, odd, even), the number at the bottom of the magic V will always be even.
- There will always be three possible magic Vs.
- If the five numbers are n, n+1, n+2, n+3, n+4, the three magic totals will be three times the middle number i.e. 3(n+2), one less than that, and one more than that. For example, for the numbers 98, 99, 100, 101, 102, the magic totals will be 299, 300 and 301.
- For any magic total, there is one, and only one, magic V.
Summing Consecutive Numbers
We're assuming that students have spent time exploring ways of expressing the numbers 9 to 15 as the sum of consecutive numbers. If you haven't had a go, you may like to try to do so now.
9 = 2 + 3 + 4
10 = 1 + 2 + 3 + 4
11 = 5 + 6
12 = 3 + 4+ 5
13 = 6 + 7
14 = 2 + 3 + 4 + 5
15 = 4 + 5 + 6
This may lead to these initial conjectures:
I think...
- All numbers can be written as the sum of consecutive numbers.
- All numbers can be written as the sum of two, three or four consecutive numbers.
- Every number can be written as the sum of consecutive numbers in only one way.
- Multiples of three can always be written as the sum of three consecutive numbers.
- Two consecutive numbers always add up to an odd total.
- Three consecutive numbers sometimes add to an odd total and sometimes add to an even total.
- Four consecutive numbers always add up to an even total.
Further testing may lead to these modified conjectures:
- All numbers, except for powers of 2, can be written as the sum of consecutive numbers.
- Every odd prime number can be written as the sum of consecutive numbers in only one way.
- Every odd prime number can be written as the sum of two consecutive numbers.
- Multiples of 3 can always be written as the sum of three consecutive numbers.
- Any odd number can be written as the sum of two consecutive numbers.
- Multiples of 3 can always be written as the sum of three consecutive numbers.
- Even numbers, that are not multiples of 4, can be written as the sum of four consecutive numbers.
- Some numbers can be expressed as the sum of consecutive numbers in more than one way.
Further exploration could lead to conjectures about multiples of 5, 6, 7...
Got It
We're assuming students have played Got It or Have You Got It? and have worked out a strategy for the default setting (target of 23, using the numbers 1 to 4). If you haven't already played, you may like to do so now.
- Let's call the totals we're aiming for 'stepping stones'.
- Begin the game by going first and choosing 3.
- Land on the following stepping stones: 8, 13, 18 to ensure you land on 23 and win.
This may lead to these initial conjectures:
I think...
- I will always win if I start.
- The 'stepping stones' that lead to a win will always alternate between odd and even.
- The distance between the 'stepping stones' will always be one more than the largest number available.
- I will always be able to figure out which number to start with to guarantee a win.
- This has something to do with factors and multiples.
- This has something to do with remainders.
Further testing may lead to these modified conjectures:
- I won't always win if I start.
- I can work out my 'stepping stones' by counting backwards from the target in steps of one more than the biggest number I can use.
- My starting number should be the remainder when I divide the target number by one more than the biggest number I can use. If the remainder is zero, I want my opponent to start.
- If the target is a multiple of one more than the biggest number I can use, then I do not want to start. Otherwise I do want to start.
Keep it Simple
Assume that students have been exploring Keep it Simple, and in particular, how to express $\frac{1}{6}$, $\frac{1}{7}$, and $\frac{1}{8}$, as the sum of two different unit fractions (fractions which have numerators of 1). If you haven't had a go, you may like to try to do so now.
$\frac{1}{6} = \frac{1}{9} + \frac{1}{18}$
$\frac{1}{7} = \frac{1}{8} + \frac{1}{56}$
$\frac{1}{8} = \frac{1}{10} + \frac{1}{40}$
This may lead to these initial conjectures:
I think...
- Every unit fraction can be written as the sum of two different unit fractions.
- Every unit fraction can be written as the sum of two different unit fractions in only one way.
- In each sum, the denominator of the smallest fraction is a multiple of the other two denominators.
Further testing may lead to these modified conjectures:
- Every unit fraction can be written as the sum of at least two different unit fractions.
- In each sum, the denominator of the smallest fraction is sometimes a multiple of the other two denominators.
- In each sum, the product of the denominators of the two largest fractions is always a multiple of the denominator of the smallest fraction.
- Every unit fraction can be written as the sum of three different unit fractions.
- Every unit fraction can be written as the sum of four, five, six... different unit fractions.
Tilted Squares
We're assuming students working on Tilted Squares can find the areas of squares drawn in their 'usual' orientation, and have drawn and found the areas of squares with a 'tilt' of 1. If you haven't worked out the areas of squares with a 'tilt' of 1, you may like to do so now. The Getting Started section offers some advice.
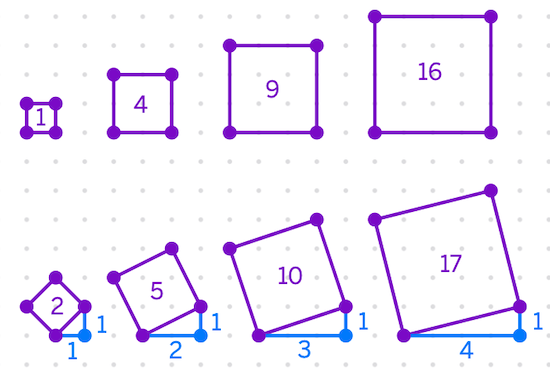
These results may lead to this initial conjecture about the areas of squares with a 'tilt' of 1:
If the base of the square goes:
1 along and 1 up, area = 2
2 along and 1 up, area = 5
3 along and 1 up, area = 10
4 along and 1 up, area = 17
So, I think if the base of the square goes
5 along and 1 up, area = 25 + 1 = 26
6 along and 1 up, area = 36 + 1 = 37
x along and 1 up, area = x$^2$ + 1
Students may draw a few more examples to convince themselves that their conjecture is valid.
This may then lead to a follow-up conjecture about the areas of squares with a 'tilt' of 2:
I think if the base of the square goes x along and 2 up, area = x$^2$ + 2
If you haven't worked out the areas of squares with a 'tilt' of 2, you may like to do so now.

These results may lead to a modified conjecture:
If the base of the square goes:
1 along and 2 up, area = 5
2 along and 2 up, area = 8
3 along and 2 up, area = 13
4 along and 2 up, area = 20
So, I think if the base of the square goes
5 along and 2 up, area = 25 + 4 = 29
6 along and 2 up, area = 36 + 4 = 40
x along and 2 up, area = x$^2$ + 2$^2$
Further exploration can lead to Pythagoras' Theorem!
Wipeout
We're assuming that students have explored Wipeout using numbers 1 to 6, and then different sets of six consecutive numbers, such as 2 to 7, 3 to 8, 15 to 20... If you haven't had a go, you may like to try to do so now.
Starting with 1 to 6, and wiping out either 1 or 6, leaves five numbers with a whole number average
Starting with 2 to 7, and wiping out either 2 or 7, leaves five numbers with a whole number average
Starting with 3 to 8, and wiping out either 3 or 8, leaves five numbers with a whole number average
Starting with 15 to 20, and wiping out either 15 or 20, leaves five numbers with a whole number average
This may lead to these initial conjectures:
I think...
- If I start with any six consecutive numbers, I will always be able to choose one of two numbers to 'wipe out' so that the five remaining numbers have a whole number average.
- If I start with any set of consecutive numbers, I will always be able to choose one of two numbers to 'wipe out' so that the remaining numbers have a whole number average.
- If I start with a large set of consecutive numbers, I will always be able to choose more than two numbers to 'wipe out' so that the remaining numbers have a whole number average.
- If I start with a random set of consecutive numbers, I can't guarantee that I will be able to find a number to 'wipe out' so that the remaining numbers have a whole number average.
Further testing may lead to these modified conjectures:
- If I have a set with an even number of consecutive numbers, I will always be able to choose one of two numbers (the lowest or the highest) to 'wipe out', so that the remaining numbers have a whole number average.
- If I have a set with an odd number of consecutive numbers, I will always be able to choose one number (the middle one) to 'wipe out', so that the remaining numbers have a whole number average.
Searching for Mean(ing)
We're assuming that students have had a chance to explore Searching for Mean(ing), and in particular, how to combine different weights so that they average 4kg. For example, combining 3kg and 8kg weights, or 3kg and 9kg weights, or 3kg and 10kg weights. If you haven't had a go, you may like to try to do so now.
3kg and 8kg weights
3, 3, 3, 3, 8 average of 4kg
3kg and 9kg weights
3, 3, 3, 3, 3, 9 average of 4kg
3kg and 10kg weights
3, 3, 3, 3, 3, 3, 10 average of 4kg
This may lead to these initial conjectures:
I think...
- If I use 3kg and 11kg weights, the following selection will give an average of 4kg: 3, 3, 3, 3, 3, 3, 3, 11
- If I use 3kg and 12kg weights, the following selection will give an average of 4kg: 3, 3, 3, 3, 3, 3, 3, 3, 12
- I will always be able to find a selection of weights with an average of 4kg if I am choosing from 3kg and one other size weight which is greater than 3kg.
- If I use 3kg and 8kg weights, I can find a selection of weights which have an average of 3kg, 4kg, 5kg, ... 8kg.
Further testing may lead to these modified conjectures:
- If I use 3kg and 8kg, then I will always be able to combine them to get a whole number average, if I choose five weights.
- If I use 3kg and xkg, then I will always be able to combine them to get a whole number average, if I choose (x-3) weights.
- There are an infinite number of ways of choosing 3kg and 8kg weights to get a whole number average between 3kg and 8kg.
- When I am given any two weights, I can always find combininations which have a whole number average between the two weights.
These collections of Primary and Secondary problems, organised by year group, are designed to encourage students to conjecture and generalise. The Teachers' Resources, which accompany each problem, suggest how students can be encouraged to use specific examples as a springboard to generalising.
Further reading and follow-up resources
Thinking Mathematically by John Mason with Leone Burton and Kaye Stacey
Learning and Doing Mathematics by John Mason
Developing a Need for Algebra by Alf Coles (for more information about 'common boards')
Podcast and transcript of Dylan Wiliam discussing effective questioning in the classroom - the conversation includes reference to a 'no hands up' approach and creating a community of learners
Thinkers by Chris Bills, Liz Bills, John Mason and Anne Watson
