Right angles
Problem
Right Angles printable sheet
Link to a collection of printable sheets of circle templates.
Can you make a right-angled triangle on this peg-board by joining up three points round the edge?
Can you work systematically to prove this?
Now try changing the number of points round the edge.
Can you do it now?
Can you show by calculation that the angle is a right angle?
Many thanks to Geoff Faux who introduced us to the merits of the 9 pin circular geo-board.
Getting Started
Try an even number of points round the edge.
Proving this will be easier if you join all the points to the centre and look for isosceles triangles.
Student Solutions
Samantha and Shummus both realised that in order to create a triangle with a right angle, the band had to go through the centre of the circle. Shummus writes:
I noticed that the bands had to be started in the centre.Xianglong Ni notes that:
If we have 9 points on the circle then you can't create a right-angle using the points. This is so because a right angle is inscribed in a semicircle; It is facing a diameter. But you can only create a diameter when there is an even amount of points on the circle. If the number of points on the circle is even then yes. If the number is odd then no.
Rachel from Newstead sent us a few diagrams to illustrate examples of right-angled triangles in circles with an even number of points.
If you haven't met this idea before, you may want to look at another problem from August 2005, Subtended angles
Here are another couple of examples of right-angled triangles using the same eight-point and ten-point circles that Rachel used:
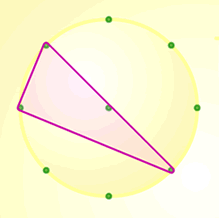
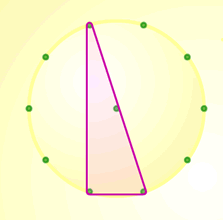
Teachers' Resources
Why do this problem?
This problem builds on Triangles in Circles and Subtended Angles . It leads to the theorem about right-angles in circles.
Teachers may find the article Angle Measurement: An Opportunity For Equity to be of interest.
Possible approach
If students will be working on paper ask them to draw right-angled triangles on their 9-peg and 12-peg circles. Alternatively, they could work on the interactive pegboard.
How many different triangles can they find?
How do they know they are right-angled?
What is special about the right-angled triangles?
Draw together conjectures which might mention the number of dots on the circle and the need to be able to join two points to form a diameter. Challenge students to justify these conjectures with convincing arguments. Eventually link this to the work on Subtended Angles .
Key questions
What do we know already that might be useful here?
What is the relationship between the angle at the centre and the angle at the circumference?
What are the implications of our findings for circles in general (without dots)?
Possible support
Students may need to spend more time convincing themselves when it is possible to make right-angled triangles. Here is a sheet with 10-peg, 12-peg and 16-peg circles to support them in investigating other cases.
Possible extension
Ask students to prove the general case.