Last Biscuit
Can you find a strategy that ensures you get to take the last biscuit in this game?
Which Spinners?
Can you work out which spinners were used to generate the frequency charts?
Vector Walk
Starting with two basic vector steps, which destinations can you reach on a vector walk?
Vector Journeys
Charlie likes to go for walks around a square park, while Alison likes to cut across diagonally. Can you find relationships between the vectors they walk along?
A Brief Introduction to Complex Numbers
In this problem, we define complex numbers and invite you to explore what happens when you add and multiply them.
A brief introduction to the Argand diagram
Complex numbers can be represented graphically using an Argand diagram. This problem explains more...
Where Are You Flying?
Where do people fly to from London? What is good and bad about these representations?
Flipping Twisty Matrices
Investigate the transformations of the plane given by the 2 by 2 matrices with entries taking all combinations of values 0, -1 and +1.
Intersections
Change one equation in this pair of simultaneous equations very slightly and there is a big change in the solution. Why?
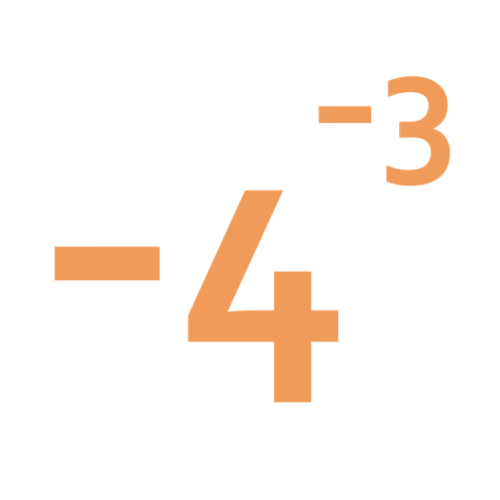
Negative Powers
What does this number mean? Which order of 1, 2, 3 and 4 makes the highest value? Which makes the lowest?
Back Fitter
10 graphs of experimental data are given. Can you use a spreadsheet to find algebraic graphs which match them closely, and thus discover the formulae most likely to govern the underlying processes?
Square Pair
Explore the shape of a square after it is transformed by the action of a matrix.

Quad in Quad
Join the midpoints of a quadrilateral to get a new quadrilateral. What is special about it?
Exploring Cubic Functions
Quadratic graphs are very familiar, but what patterns can you explore with cubics?
Equation Attack
The equation a^x + b^x = 1 can be solved algebraically in special cases but in general it can only be solved by numerical methods.
Root Hunter
In this short problem, try to find the location of the roots of some unusual functions by finding where they change sign.
Gradient Match
What can you deduce about the gradients of curves linking (0,0), (8,8) and (4,6)?
Turning to Calculus
Get started with calculus by exploring the connections between the sign of a curve and the sign of its gradient.
Proving the Laws of Logarithms
Here you have an opportunity to explore the proofs of the laws of logarithms.
Three by One
There are many different methods to solve this geometrical problem - how many can you find?
What Do Functions Do for Tiny X?
Looking at small values of functions. Motivating the existence of the Maclaurin expansion.
It's Only a Minus Sign
Solve these differential equations to see how a minus sign can change the answer

Farey Neighbours
Farey sequences are lists of fractions in ascending order of magnitude. Can you prove that in every Farey sequence there is a special relationship between Farey neighbours?
Inverting Rational Functions
Consider these questions concerning inverting rational functions
Polite Numbers
Folium of Descartes
Investigate the family of graphs given by the equation x^3+y^3=3axy for different values of the constant a.
