A brief introduction to the Argand diagram
Complex numbers can be represented graphically using an Argand diagram. This problem explains more...
Problem
This problem follows on from A Brief Introduction to Complex Numbers
Watch the video below to learn about the Argand diagram.
If you can't see the video, reveal the hidden text which describes the video
Complex numbers can be represented on an Argand diagram. The real part of a number corresponds to the $x$ coordinate and the imaginary part of a number corresponds to the $y$ coordinate. So the number $z=x+iy$ would be represented by the point $(x,y)$.
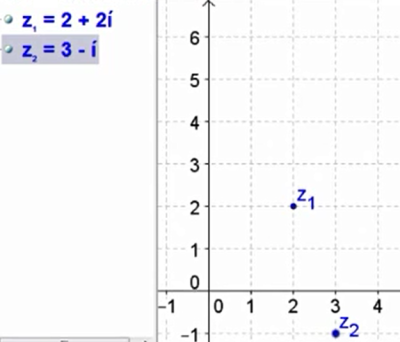
The Argand diagram below shows the numbers $z_1=2+2i$ and $z_2=3-i$.
You can explore the Argand diagram using GeoGebra, a free-to-download graphing package.
We have created an online GeoGebra worksheet for you to explore the questions below.
Let $z_1$ and $z_2$ be complex numbers represented on an Argand diagram, and let $z_3$ be their product.
Fix $z_1$, and move $z_2$ until $z_3$ is on the x-axis.
What can you say about the trajectory of $z_2$ as you move it to keep $z_3$ on the x-axis?
Repeat the above for other values of $z_1$, keeping a record of the values of $z_2$ and $z_3$.
- In each case, can you make predictions about where $z_2$ needs to be for $z_3$ to be on the x-axis?
- Can you predict where $z_2$ needs to be when you want $z_3$ to be at a given point on the x-axis?
Can you use algebra to explain why the values of $z_2$ you found for each $z_1$ give real values for $z_3$?
Now carry out the same process but this time aiming to keep $z_3$ on the y-axis.
You may want to have a go at Complex Squares next.
Getting Started
Pick a point for $z_1$ such as $2+i$. Move $z_2$ around, and keep a record of the points where $z_3$ is on the x-axis. What do you notice about the coordinates of $z_2$ and $z_3$?
Repeat for some other points.
Student Solutions
Vanessa and Annie sent us this solution:
Fixing $z_1$ then moving $z_2$ so that $z_3$ is on the x-axis:
We tried this for several different values of $z_1$. Here is what we found:
- For $z_1=2+2i$, we think you need $z_2$ to be on the line $y=-x$. So $z_2=c(1-i)$ for any $c$.
- For $z_1=1+2i$, we think you need $z_2$ to be on the line $y=-2x$. So $z_2=c(1-2i)$.
- For $z_1=2-i$, we think you need $z_2$ to be on the line $y=-\frac{1}{2x}$. So $z_2=c(2+i)$.
- For $z_1=4+3i$, we think you need $z_2$ to be on the line $y=-\frac{3}{4} x$. So $z_2=c(4-3i)$.
We think generally if you have $z_1=a+bi$, then you need $z_2=c(a-bi)$.
We also tried keeping $z_3$ on the $y$-axis. We tried this for the same values of $z_1$. Here is what we found:
- For $z_1=2+2i$, we think you need $z_2$ to be on the line $y=x$. So $z_2=c(1+i)$ for any $c$.
- For $z_1=1+2i$, we think you need $z_2$ to be on the line $y=\frac{1}{2}x$. So $z_2=c(2+i)$.
- For $z_1=2-i$, we think you need $z_2$ to be on the line $y=2x$. So $z_2=c(-1+2i)$.
- For $z_1=4+3i$, we think you need $z_2$ to be on the line $y=\frac{4}{3} x$. So $z_2=c(3+4i)$.
We think generally if you have $z_1=a+bi$, then you need $z_2=c(b+ai)$.
Sam sent in this algebraic explanation:
Set $z_1=a+bi$, $z_2=c+di$.
Then $z_3=z_1\, z_2=(a+bi)(c+di)=(ac-bd)+(ad+bc)i$.
As $z_3$ lies on the $x$-axis, $Im(z_3)=0$, so let the given point on the $x$-axis be
$m$ (i.e. $Re(z_3)=m$).
Then we have $ac-bd=m$ and $ad+bc=0$.
$\Rightarrow \, c=\frac{-ad}{b}$.
Substitute this into $ac-bd=m$:
$$m=-\frac{a^2 d}{b}-bd = \frac{-(a^2+b^2)d}{b}$$
$$\Rightarrow d=\frac{-mb}{a^2+b^2}.$$
Substitute this into $\frac{-ad}{b}=c$ to get
$$c=\frac{ma}{a^2+b^2}.$$
So for $z_3=z_1\, z_2=m$ and $z_1=a+bi$,
$$z_2=\frac{ma}{a^2+b^2}-\frac{mb}{a^2+b^2}i = \frac{m}{a^2+b^2}(a-bi).$$
So $z_2$ will always be a scalar multiplied by $a-bi$. This means it will have
the same trajectory as $z_1$ reflected about the $x$-axis.
Similarly, if you want to have $z_3=n$, where $n$ is on the $y$-axis, and $z_1=a+bi$, then you need to have $$z_2=\frac{n}{a^2+b^2}(b+ai).$$
Well done everyone!
Teachers' Resources
Why do this problem?
This problem is a suitable follow-up to A Brief Introduction to Complex Numbers to encourage students to explore the Argand diagram and get a feel for what happens geometrically when we multiply complex numbers.
Possible approach
Students will need computers to access the online GeoGebra worksheet, or to recreate the worksheet for themselves with the free open-source GeoGebra software or an alternative graphing package.
Show students the video to introduce the Argand diagram and the complex numbers functions in GeoGebra.
Then invite students to explore the questions posed:
Fix $z_1$, and move $z_2$ until $z_3$ is on the x-axis. What can you say about the trajectory of $z_2$ as you move it to keep $z_3$ on the x-axis?
Repeat the above for other values of $z_1$:
- In each case, can you make predictions about where $z_2$ needs to be for $z_3$ to be on the x-axis?
- Can you predict where $z_2$ needs to be when you want $z_3$ to be at a given point on the x-axis?
Once students have had a chance to explore with GeoGebra, bring the class together to share what they have found:
"Can you use algebra to explain why the values of $z_2$ you found for each $z_1$ give real values for $z_3$?"
Students can also explore what happens when they try to keep $z_3$ on the y-axis.
Key questions
What can be said about the complex number $z_3=x+iy$ if it lies on the x-axis?
If $z_1$ is at the point $a+ib$, what can be said about the point $z_2$ in order for $z_3$ to be on the x-axis?
Possible extension
Once students have grasped the Argand diagram, they could try Complex Squares.
Possible support
Ask students to pick a point for $z_1$ such as $2+i$, move $z_2$ around, and keep a record of the points where $z_3$ is on the x-axis. What do they notice about the coordinates of $z_2$ and $z_3$?
Suggest they repeat for some other points and share their results.
