The Koch snowflake

Explore the strange geometrical properties of the Koch Snowflake.

Age

16 to 18

Challenge level

Being curious Being collaborative Being resourceful Being resilient

Problem

The Koch Snowflake is made by repeating the following process.

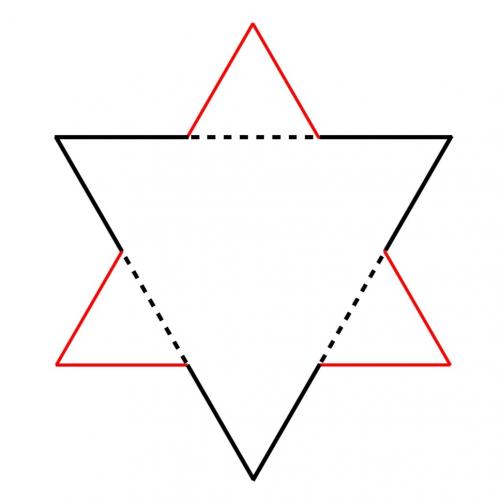
Start with an equilateral triangle. Split each side into three equal parts, and replace the middle third of each side with the other two sides of an equilateral triangle constructed on this part. The diagram below shows this step, with the original equilateral triangle in black, and the middle third of each side (the dotted part) being replaced with two red sides.

The shape created from the description above.

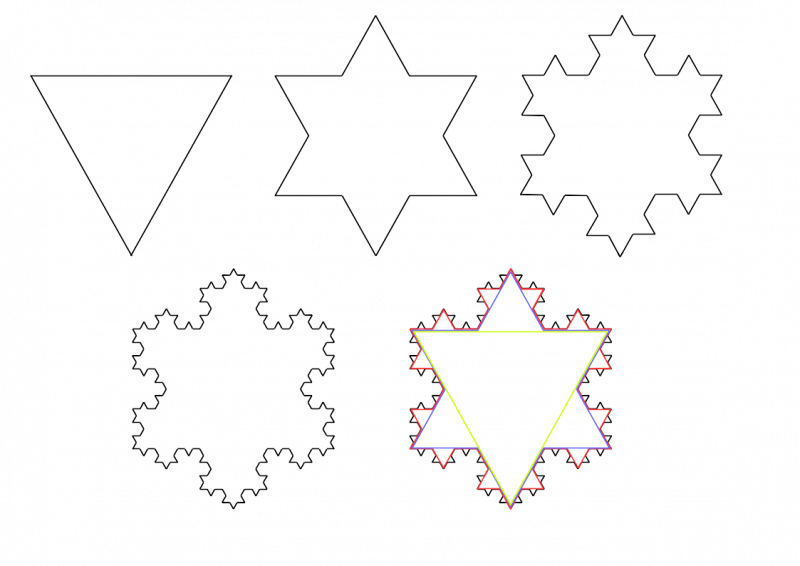
This process is then repeated, with each straight edge being split into three and the middle third at each stage being replaced by the other two sides of an equilateral triangle constructed on this section of the line. The diagram below shows the first 4 shapes in the process, as well as a picture showing all four superimposed on each other.

The first four shapes in the process described above, and then all four shapes superimposed.

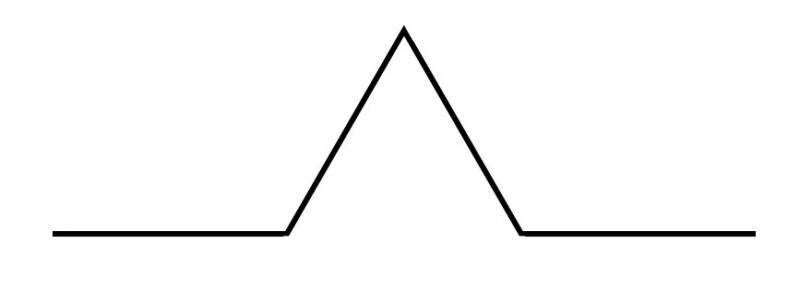
A different way of thinking about this process is to notice that at each stage every straight line is replaced by a line that looks like this:

A black line forming a symmetrical triangular peak in the centre, with horizontal lines extending from both ends.

The Koch Snowflake Curve is the shape you get if you continue this process forever. The video below shows the first six stages of the infinite process for generating the Koch snowflake.

Here are some questions about the Koch Snowflake.

There are three edges in the first iteration of the snowflake. How many edges are there in the second iteration? How many in the third iteration?
Find a formula for the total number of edges of the $n^{\text {th}}$ iteration.
If the first iteration has edges of length 1, how long are the edges in iteration 2?
Find a formula for the length of each edge in the $n^{\text {th}}$ iteration.
Use your results to find a formula for the total length of the $n^{\text{th}}$ iteration of the snowflake. What happens to the length of the snowflake as $n$ gets larger?

Now consider the area of the Koch Snowflake.

Let the area of the first iteration be $A$ (you might be able to actually calculate $A$ given that you know the lengths of the edges). What is the extra area added on by each extra triangle in the second iteration?
This diagram might help! Remember that the original triangle has area $A$.

Image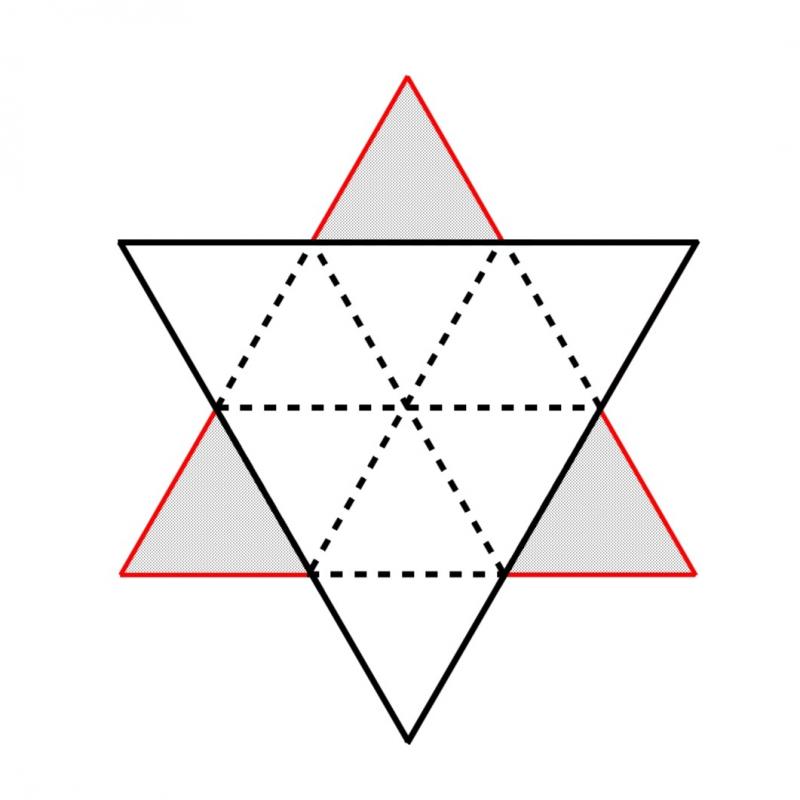
How much area in total is added by the second iteration?
How much area is added by the third iteration?
Can you find an infinite sum for the area of the Koch Snowflake? Can you simplify this?
It might be easier to work out separately the size of each extra triangle at each stage and also the number of triangles added each time. These can then be combined to give the extra area added each time.

How do the length and the area behave as the number of sides increase?

The Koch Snowflake is an example of a fractal. It is a "self similar" shape, which means that when you zoom into a side the shape still looks as complicated as the original shape. If you keep zooming into the Koch Snowflake you will never get a straight line or a curve, you will always see "spikes". The Koch Snowflake has a larger dimension than a 1D straight line, but smaller than that of a 2D shape: in fact the dimension of the Koch Snowflake is given by $\frac{\log 4}{\log 3} = 1.26...$.

There are lots of different fractals you can explore. You might like to try the Nrich problems Squareflake and Sierpinski Triangle.

In this video Claire and Charlie discuss how the Mandelbrot Set is generated. This is probably the most famous fractal!

Student Solutions

Thank you to everyone who sent in solutions for this problem.

We had several solutions from students at London Academy of Excellence Tottenham (LAET) in the UK. Matusala, Abdisamad, Jin Hao, Maria, Malaika and Elliot explored the side lengths and total perimeter for the first few iterations of the snowflake. Here is Abdisamad's summary:

3 edges in the first iteration, 12 in the second iteration, 48 in the third iteration.
3, 12, 48, etc. The next iteration is 4 times more than the previous iteration, therefore the $n$th iteration should be $3\times 4^{n-1}$.
Length of 1 in the first iteration, $\dfrac{1}{3}$ in the second iteration, $\dfrac{1}{9}$ in the third iteration, etc.
$1, \dfrac{1}{3},\dfrac{1}{9}$ etc. The next iteration is 3 times less than the previous iteration, therefore the $n$th iteration should be $1\times \left(\dfrac{1}{3}\right)^{n-1}$.
To find the total length, it should be both formulas put together, therefore the total length of the $n$th iteration should be $\left(3\times 4^{n-1}\right)\left(1\times \left(\dfrac{1}{3}\right)^{n-1}\right)$ which simplifies to $3 \times \left(\dfrac{4}{3}\right)^{n-1}$.

Maria used diagrams to help explain her argument. Here is her work.

Thatcher from Rugby School UK and China, Prasangi from Bronx High School of Science in New York, Yash from Tanglin Trust School in Singapore, Nishad from Thomas Estley Community College, William from Simon Balle All-through School in the UK, Ci Hui Minh Ngoc Ong from Kelvin Grove State College (Brisbane) in Austrialia, Emily from Bishop's Wordsworth's Grammar School in the UK and Samuel, Kawthar and Kim from LAET used a formula to investigate the perimeter. Here is Samuel's work:

Nishad simplified the formula and commented on what happens in the long term:

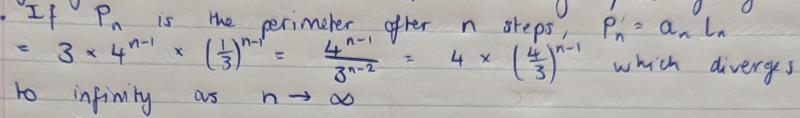
Prasangi, Maria, Malaika, Elliot, Thatcher, Yash, Nishad, William, Ci Hui Minh Ngoc Ong, Emily, Samuel, Kawthar and Kim also investigated the areas of the triangles. This is William's explanation of the areas of the triangles added in the first two iterations (click to enlarge):

Prasangi, Thatcher, Nishad, William and Ci Hui Minh Ngoc Ong continued in this way to find the total area of each iteration. This is Nishad's work:

Yash, Emily, Samuel, Kawthar and Kim did the same, but used numbers rather than $A$ for the areas. This is Emily's work (you can click on the image of Emily's work to see a larger version):

Thatcher compiled their work into a full paper. Click here to see Thatcher's work.

Ci Hui Ming Ngoc Ong put the formulas for the side lengths and areas into a spreadsheet to calculate them automatically (click on the image to see more rows):

Ci Hui Minh Ngoc Ong then used the spreadsheet to create graphs showing how the side lengths, perimeter, small triangle area and total area change with more iterations: