Squareflake
Problem
The diagram below shows Stage $0$ (the red square) and Stage $1$ in the sequence of curves which leads to the squareflake fractal when the process described below is repeated infinitely often. If the original square has side $1$ unit at what stage does the length of the curve begin to exceed $1$ million units? What is the area contained within the fractal curve, what is the length of the curve
and what is the dimension of the fractal? What follows is simply information to help you solve this problem.
The rule for generating the squareflake fractal curve is to replace each line segment by the zig-zag curve shown above on the right, called the generator. Notice that the generator is made up of $8$ line segments, each one quarter the original length.
Image
|
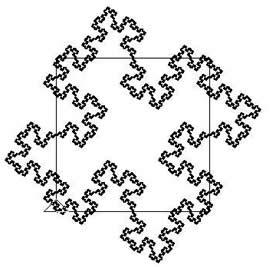
The curve on the left shows Stage $5$ of the sequence with the Stage $0$ square superimposed but this is not a fractal, it is still early on in the process of forming the fractal. The squareflake fractal contains self similar copies of itself. No matter how much you magnify the fractal curve, zooming in on it, you always see the same structure containing smaller and smaller copies of itself.
[If you want to draw fractals for yourself click here to see the Logo program which was used to draw this fractal and for information about downloading a free version of Logo. See First Forward for a twelve part series introducing Logo programming for beginners.] |
This problem asks you to work out the dimension of the fractal. To do this you need to use the formula $n=m^d$ where $n$ is the number of copies in the generator of the line segment it replaces, $m$ is the magnification factor, and $d$ is the dimension. (Click here to read how this formula for dimension applies to the dimensions of a line, a
square and a cube.)
Getting Started
Student Solutions
Jeremy of Drexel University and Andrei of Tudor Vianu National College, Bucharest, Romania sent in excellent solutions. The first half of this solution is Andrei's, the second Jeremy's.
To solve this problem, I made a table with the length and the area of the fractal at the first stages:
| Stage | Length | Area |
| 0 | 4 | 1 |
| 1 | $4\times2=8$ | 1 |
| 2 | $4\times2^2=16$ | 1 |
|
I have made the following observations:
The length of the fractal at each stage is twice its length at
the preceding stage.
The area of the fractal is constant because the two colored
areas are equal (the blue one is added, the yellow one
subtracted)
For the $n^{th}$ stage the length of the curve is $4 \times 2^n =2^{n+2}$ and the area is $1$ square unit |
Image

|
Now we have the curve length for any stage $n$, and in turn, a stage $n$ for any particular curve length. \begin{eqnarray} 1,000,000 &=& 2^{n + 2}\\ n &=& log_2 (1,000,000) - 2 \\ n &\approx& 17.9 \end{eqnarray} Because 17 < n < 18 , the length must have been less than $1,000,000$ at stage $17$ and greater than $1,000,000$ at stage $18$. Thus answers the question: stage $18$. Further, we can now find the exact lengths of the curve at stage $17$ and stage $18$ to convince ourselves: $$L(17) = 2^{17 + 2} = 2^{19} = 524,288$$ which is less than $1,000,000$ $$L(18) = 2^{18 + 2} = 2^{20} = 1,048,576$$ which is greater than $1,000,000$.
The length of the fractal is $$\lim_{n\to \infty} 2^{n+2}$$ and hence the fractal curve has infinite length. This is an example of a curve of infinite length surrounding a finite area.
What is the dimension of the fractal? Solution: $d = 1.5$
Explanation: the dimension $d$ is given by the formula $n = m^d$.
$n = 8$ because each segment is broken up into 8 self-similar segments.
$m = 4$ because each of the $8$ new segments is $1/4$ the length of the original segment, and thus must be multiplied by $4$ to be the length of the original segment.
So: $8 = 4^d$ and hence $d = log_4 8 = 1.5$.
Teachers' Resources
Imagine breaking a cube into 64 identical small cubes. The length of the edge of the big cube is 4 times the length of the edge of a small cube and we say that the magnification factor is 4. As $64=4^3$ we see that the number of small self similar pieces is equal to the magnification factor cubed. The number 3 is called the dimension of the cube.
If you break a line of length 1 into self similar bits of length ${1\over m}$ there are $m^1$ bits and the dimension of the line is 1.
If you break up a square of side 1 into self similar squares with edge ${1\over m}$ then there are $m^2$ smaller squares and the dimension is 2.
If you break up a cube of side 1 into self similar cubes with edge ${1\over m}$ then there are $m^3$ smaller cubes and the dimension is 3.
In each case we say the magnification factor is $m$ meaning that we have to scale the lengths by a factor of $m$ to produce the original shape. The formula for dimension is: $n = m^d$ where $n$ is the number of self similar bits, and $d$ is the dimension.
We can generalise what we know about 1, 2 and 3 dimensions to the non integer dimensions of fractals using the formula (where d is the dimension): $$\text{number of self similar bits} = \text{(magnification factor})^d.$$
You can download a free copy of MSW Logo from http://www.softronix.com/logo.html
This is the program that draws the squareflake.
to flake :side :stage
repeat 4[line :side :stage rt 90]
end
to line :side :stage
if :stage = 0 [fd :side stop]
line :side /4 :stage - 1 lt 90
line :side /4 :stage - 1 rt 90
line :side /4 :stage - 1 rt 90
repeat 2 [line :side /4 :stage - 1] lt 90
line :side /4 :stage - 1 lt 90
line :side /4 :stage - 1 rt 90
line :side /4 :stage - 1
end
