Simply Graphs
Look for the common features in these graphs. Which graphs belong together?
Problem
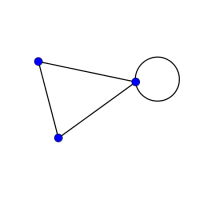
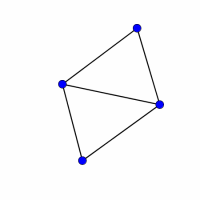
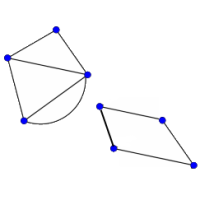
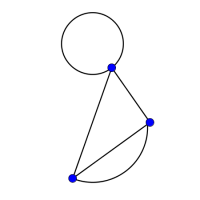
A graph is a set of vertices (or nodes), together with a set of edges (or arcs).
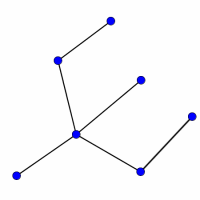
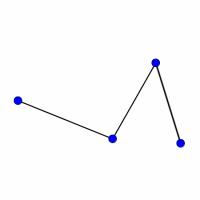
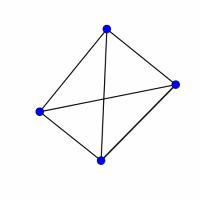
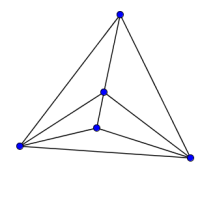
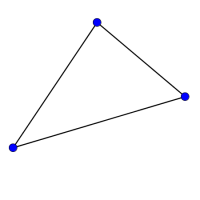
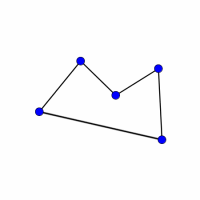
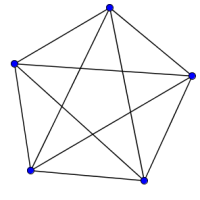
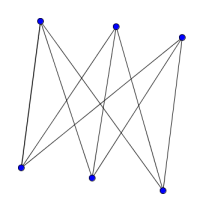
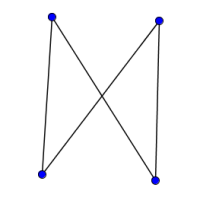
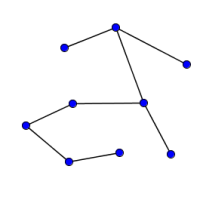
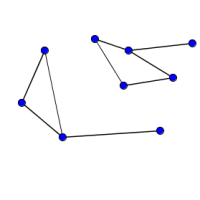
Look at the graphs below. You can print them off as a set of cards here.
Image
|
Image
|
Image
|
Image
|
Image
|
Image
|
Image
|
Image
|
Image
|
Image
|
Image
|
Image
|
Image
|
Image
|
Image
|
Can you find graphs that you think 'belong' together in some sense?
Can you describe the features they have in common?
Could you draw more graphs that 'belong' in the same set?
Click below to see some definitions used to describe graphs.
- A loop is an edge with the same vertex at both ends.
- A simple graph has no loops, and there is no more than one edge connecting any pair of vertices. A multigraph has multiple edges connecting some pairs of vertices.
- A walk is a sequence of edges in which the end of one edge (except the last) is the beginning of the next.
- A trail is a walk in which no edge is repeated.
- A path is a trail in which no vertex is repeated.
- A cycle is a closed path (the end of the last edge is the start of the first).
- A Hamiltonian cycle visits every vertex.
- A connected graph has a path between every pair of vertices.
- A tree is a simple connected graph with no cycles.
- A complete graph is a simple graph where every pair of vertices is connected by an edge.
Can you find examples on the cards that match each definition? Can you draw some more examples of your own?
Getting Started
What is it about some graphs that make them similar to others?
Can you think of different properties of the graphs?
Can you trace routes from one node to another?
Can you think of different properties of the graphs?
Can you trace routes from one node to another?
Student Solutions
Vanessa and Annie sent us this solution:
We labelled the graphs like this:
1 2 3
4 5 6
7 8 9
10 11 12
13 14 15
We grouped the graphs like this:
We noticed that graphs 7,9,10,11,12 and 13 had the same number of edges coming out of each vertex.
We also looked at which graphs you could draw without taking your pencil off the paper and without drawing the same line twice. We found out this is called traceability. Graphs 1,9,10,11,13 are traceable, starting and finishing at the same point. Graphs 2,4,6,8 are traceable, starting and finishing at different points. The other graphs are not traceable.
We checked this by counting the number of edges coming out of each vertex. If you want to start and finish at the same point, this number must be even for all the vertices in the graph. This is because every time you arrive at the vertex by one edge you need to be able to leave it by another. If you want to start and finish at different points, you need two (but only two) odd vertices. This is because the first vertex has an 'exit' edge without a corresponding 'entry' edge and vice versa for the last vertex. If you have 1 or more than 2 vertices with an odd number of edges, the graph is not traceable.
Well done! Can you think of any other interesting properties or ways to group the graphs?
We labelled the graphs like this:
1 2 3
4 5 6
7 8 9
10 11 12
13 14 15
We grouped the graphs like this:
- Graphs with loops (1 and 4) and graphs without loops (all the other graphs).
- Non-simple graphs (1,3,4) and simple graphs (all the other graphs).
- Non-connected graphs (3, 15) and connected graphs (all the other graphs).
- Trees (14,5,6) and non-trees (all the other graphs).
- Complete graphs (11,7,9) and non-complete graphs (all the other graphs)
We noticed that graphs 7,9,10,11,12 and 13 had the same number of edges coming out of each vertex.
We also looked at which graphs you could draw without taking your pencil off the paper and without drawing the same line twice. We found out this is called traceability. Graphs 1,9,10,11,13 are traceable, starting and finishing at the same point. Graphs 2,4,6,8 are traceable, starting and finishing at different points. The other graphs are not traceable.
We checked this by counting the number of edges coming out of each vertex. If you want to start and finish at the same point, this number must be even for all the vertices in the graph. This is because every time you arrive at the vertex by one edge you need to be able to leave it by another. If you want to start and finish at different points, you need two (but only two) odd vertices. This is because the first vertex has an 'exit' edge without a corresponding 'entry' edge and vice versa for the last vertex. If you have 1 or more than 2 vertices with an odd number of edges, the graph is not traceable.
Well done! Can you think of any other interesting properties or ways to group the graphs?
Teachers' Resources
Why do this problem?
Introductions to graph theory can often end up being quite dry and dusty, with lots of definitions that need to be memorised. This problem invites students to engage with the different types of graph as a pictorial representation so that they can understand why different categorisations are necessary.Possible approach
Hand out the cards."Here is a set of cards. Each card shows a representation of a graph. A graph is a collection of vertices, also called nodes, joined by edges, also called arcs. Sort the cards into groups that you think belong together in some way, and sketch the graphs together with an explanation of why you have sorted them together. See how many different ways of categorising the graphs you can come up with."
While students are working, circulate and look out for groups who have come up with collections of graphs that fit standard definitions. Here are some definitions that might be appropriate.
Bring the class together and share the categorisations they came up with. When they identify a standard categorisation, share the usual terminology with them. Perhaps hand out the definitions sheet and invite them to find examples on the cards for each definition.
Key questions
What is it about some graphs that make them similar to others?Can you think of different properties of the graphs?
Can you trace routes from one node to another?
