Euler's Formula
In this article, we shall prove Euler's Formula for graphs, and then suggest why it is true for polyhedra. (Don't panic if you don't know what Euler's Formula is; all will be revealed shortly!) If you haven't met the idea of a graph before (or even if you have!), you might like to have a look here . I am also going to assume for the main proof that you are familiar with the idea of induction, although you may still be able to get the idea of the article without being.
As explained in the article referred to above, a graph is a mathematical object consisting of points (vertices) and lines (edges) joining some or all of the pairs of vertices. The lines may be curved, and may overlap, but may only intersect at vertices.
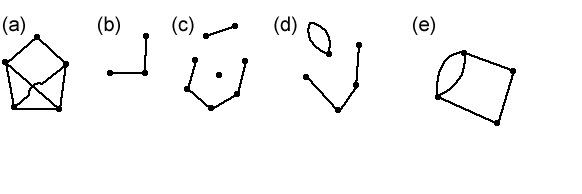
I am going to impose two additional restrictions, namely that a graph may not contain any loops (edges from a vertex back to the same vertex) or multiple edges (between any two vertices, there may be at most one edge). So graphs (d) and (e) above are not allowed. Some writers call graphs with these restrictions simple graphs , but since they are the only graphs we shall be using in this article, when I say "graph" I shall always mean "simple graph". Another useful concept is that of connectedness. A graph is connected if, given any two vertices, there is a path from one to the other in the graph (that is, an ant starting at any vertex can walk along edges of the graph to get to any other vertex). So graphs (a) and (b) above are connected, but graph (c) is not.
Imagine that you are at a party with some other people. You have a pile of ribbons. Your task is to arrange yourselves and the ribbons in such a way that there is a ribbon between each pair of people (that is, any two people are holding opposite ends of a ribbon), and none of the ribbons overlap. (Don't forget that ribbons can bend, and you are allowed to assume that they're as long as you like for this particular game!) This would be easy if there were only three of you:
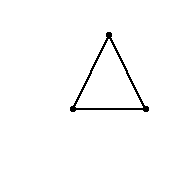
Can you do it if there are four of you? What about five? You should try to either explicitly explain how to do it (by drawing a diagram like the one above), or prove that it can't be done.
Here's a slightly different party game. This time, there are the same number of girls as boys at the party. Now you have to arrange yourselves so that there's a ribbon between each girl and each boy (but we don't have any girls sharing a ribbon, or any boys sharing a ribbon). Again, you have to try to do this so that the ribbons don't overlap. This would be easy if there were only two girls and two boys:
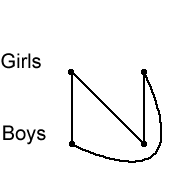
What if there are three girls and three boys? Or four? Again, try to give a way to do it or prove that it can't be done.
Hopefully you've seen by now how these questions relate to graph theory. We are asked to draw certain graphs such that none of the edges overlap. We call the graph with $n$ vertices and every possible edge (that is, any two vertices are joined), the complete graph on $n$ vertices, and write this as $K_n$; for example, $K_3$ is the triangle shown above. So the first game was asking us to draw $K_4$ and $K_5$ in such a way that the edges don't overlap.
We also have a name for the graphs we tried to find in the second game. By a bipartite graph , we mean a graph such that we can split the vertices into two groups, $A$ and $B$, say, so that every edge is from a vertex in $A$ to a vertex in $B$. Graphs (a), (b) and (d) below are bipartite; graph (c) is not.
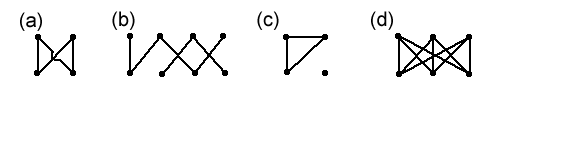
You can probably guess what the complete bipartite graph on $2n$ vertices is: it's the bipartite graph with $n$ vertices in each class ($n$ in $A$ and $n$ in $B$, if you like) with all of the edges between the classes (as shown in (a) and (d) in the above diagram). We write this as $K_{n,n}$.
You should have discovered that you can draw $K_4$ without overlaps. One way of doing this is shown in the Solutions. We say that $K_4$ is planar , meaning that it can be drawn in the plane (on a flat piece of paper) without any overlaps. Is $K_5$ or $K_{3,3}$ planar? The answer is no. But it's not clear how we can prove this - this is where Euler's formula will be useful.
Just before I tell you what Euler's formula is, I need to tell you what a face of a plane graph is. A plane graph is a drawing of a planar graph. A face is a region between edges of a plane graph that doesn't have any edges in it. (We don't talk about faces of a graph unless the graph is drawn without any overlaps.) For example, each face of this graph is coloured differently:
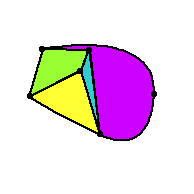
Don't forget that the bit around the outside of the graph counts as a face too (it's coloured white in the above diagram).
Theorem: Let $G$ be a planar, connected graph. Let $V$ be the number of vertices, $E$ the number of edges, and $F$ the number of faces in $G$. Then $V-E+F=2$.
The first time I saw this, it seemed quite amazing to me. No matter what graph I draw, as long as the graph is planar and connected, this number $V-E+F$ is always the same! It's not even obvious that this number will always be the same for any given graph. For example, we've shown that we can draw $K_4$ without any overlaps. If you count up, you'll find that $V-E+F=2$. But why isn't there a different way of drawing it where $V-E+F$ is something else? That's what makes this theorem so remarkable.
The theorem can be proved using induction on the number of edges; if you don't know about induction, then you might not be able to follow the proof.
If the graph has $E=0$ or $E=1$, then the requirement that it be connected tells us exactly what the graph looks like (either a point, or an edge with a vertex at each end), and we can very easily check that $V-E+F=2$ ($F=1$ in both cases).
Let us now suppose that the result is true for any graph with at most $k$ edges, and consider a graph with $E=k+1$. We have to be slightly careful at this point: what we'd like to do is to remove one edge, see what happens to the number of faces, and use the inductive hypothesis. However, it is possible that removing an edge would disconnect the graph, like this, for example:
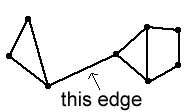
Pick an edge. Let us first consider what happens if removing the edge disconnects the graph. In this case, the number of faces does not change, since the edge must have bounded the same face on either side. However, we have to be slightly careful about the inductive hypothesis: we now have two connected subgraphs, and can apply the hypothesis to each of them separately, but we must remember that this will count the infinite outside face twice, when we only want it once. Say there are $V_1$ vertices in one graph, with $E_1$ edges and $F_1$ faces, and similarly $V_2$, $E_2$ and $F_2$ for the other subgraph. Then we have $V_1-E_1+F_1=2$ and $V_2-E_2+F_2=2$, so $V_1+V_2-E_1-E_2+F_1+F_2=4$. Now $V=V_1+V_2$, $E=E_1+E_2+1$ (remember the edge we removed?), and $F=F_1+F_2-1$, so $V-(E-1)+F+1=4$, that is, $V-E+F=2$.
Things are more a bit simpler in the other case, when removing the edge does not disconnect the graph. Here the edge must have bounded two faces, which will merge to become one. So, applying the inductive hypothesis to this new graph, we have $V-(E-1)+(F-1)=2$, and so $V-E+F=2$. In other words, if the formula is true for $E\leq k$, then it is also true for $E=k+1$, and so the result is proved, by mathematical induction.
Let's see how we can use this result to show that $K_5$ is non-planar , by first proving an inequality that holds for certain planar graphs.
Take a connected plane graph (remember, that's a graph drawn with no overlapping edges). We're only going to consider graphs where each edge bounds exactly two faces, so the example above of where removing an edge could disconnect the graph would not be allowed.
Each face is bounded by some number of edges. Let $F_i$ be the number of faces bounded by $i$ edges. Then $\sum_{i=3}^{\infty} F_i = F$ (as every face is bounded by at least three edges). Also, each edge bounds exactly two faces, so we must have $\sum_{i=3}^{\infty} i F_i =2E$ (the sum counts the number of edges, but counts each edge twice). Since the sum starts at $i=3$, we have $2E=\sum_{i=3}^{\infty} i F_i\geq \sum_{i=3}^{\infty} 3F_i = 3F$, so $F\leq \frac{2E}{3}$. Now let's put this into Euler's formula, and see what we get. Well, $2=V-E+F\leq V-E+\frac{2E}{3}$, so we get $E\leq 3(V-2)$ (multiply it out to check this yourself!). So we know that if we have a connected planar graph where each edge bounds exactly two faces, then we must have $E\leq 3(V-2)$. (However, we might be able to find a connected graph that has $E\leq 3(V-2)$ but is not planar: we haven't shown anything about this.)
Now $K_5$ has $5$ vertices, and $10$ edges (you should check this: remember that each vertex is joined to all the other vertices, but be careful not to count edges twice). But $3\times(5-2)=9$ and this is less than the number of edges, so $K_5$ cannot possibly be planar.
Can we use this same method to show that $K_{3,3}$ is non-planar? Try it and see. You might like to find a graph with the same number of edges and vertices as $K_{3,3}$ that is planar (of course, it won't be bipartite!)
In fact, it is possible to use a very similar technique, but to do so, we need to know a little bit more about bipartite graphs. A cycle is a closed loop in a graph, so an ant can start at a vertex in the cycle, and crawl round the cycle, never repeating edges or vertices, until it gets back to the start. It turns out that a graph is bipartite if and only if it contains no odd cycles (cycles with an odd number of edges). You might like to try to prove this for yourself; I'm not going to give details here. As a consequence ofthis, any face in a bipartite plane graph must be bounded by at least $4$ edges. So we can slightly alter our inequality above: $2E=\sum_{i=4}^{\infty} i F_i\geq \sum_{i=4}^{\infty} 4F_i=4F$, so $F\leq\frac{2E}{4}=\frac{E}{2}$. Now we use Euler's formula in the same way as before, to get $2\leq V-E+\frac{E}{2}$ so $E\leq 2(V-2)$. What happens if we try $K_{3,3}$? Well, $K_{3,3}$ has $6$ vertices and $9$ edges, but $2\times (6-2)=8$ and $8$ is less than $9$, so this shows that $K_{3,3}$ is non-planar.
There's one final aspect of Euler's formula that I'm going to mention in this article, and that's to do with polyhedra. If you can, get (or make!) some models of polyhedra, so that you can see for yourself that what I'm about to say works. Euler's formula applies to polyhedra too: if you count the number $V$ of vertices (corners), the number $E$ of edges, and the number $F$ of faces, you'll find that $V-E+F=2$. For example, a cube has 8 vertices, $12$ edges and $6$ faces, and sure enough, $8-12+6-2$. Try it out with some other polyhedra yourself.
Why does this same formula work in two seemingly different contexts? Here's a way to imagine it (don't try this at home!). Take your polyhedron, and suppose that it's made out of some incredibly stretchy rubber. Take a needle, and 'pop' the polyhedron in the middle of one of the faces. Now stretch out the rubber, stretching the hole where you've popped it, but being very careful to make sure that the hole stays 'within' the face. If you keep stretching it correctly, you'll end up with a flat graph - the edges of the graph are the edges of the polyhedron, and that infinite outside face we kept trying not to forget earlier is the face that we popped! One helpful tool in visualising this is the Schlegel graph . You can find out what this is, and explore what it looks like for some well known solids, in the Icosian Game.
This is not a proof, but hopefully it gives you an intuitive idea of why these situations are related.
