Inequalities
Which of the statements must be true?
Problem
For any real numbers $a$, $b$, and $c$ where $a \ge b$, consider these statements:
- $-b \ge -a$
- $a^2 + b^2 \ge 2ab$
- $ac \ge bc$
Which of the statements 1, 2, and 3 must be true?
(A) None of them
(B) Statement 1 only
(C) Statement 2 only
(D) Statement 3 only
(E) Statements 1 & 2 only
(F) Statements 1 & 3 only
(G) Statements 2 & 3 only
(H) Statements 1, 2 and 3
This question comes from TMUA Specimen paper 2.
The Test of Mathematics for University Admission (or TMUA) is designed to give you the opportunity to demonstrate that you have the essential mathematical thinking and reasoning skills needed for a demanding undergraduate Mathematics or Mathematics-related course. There are several UK universities which encourage their applicants to sit TMUA, and a good performance may result in a reduced offer.
For more information about TMUA visit https://esat-tmua.ac.uk/about-the-tests/tmua-test/.
Student Solutions
Yazan from Dubai International Academy in the United Arab Emirates explained statement 1 must be true, assuming $a$ and $b$ are positive:
Statement 1 ($-b \ge -a$) is correct because $a$ has a higher value than $b$, so if you put a negative sign before both of them, $-b$ will be higher, because the higher the value of the number after the negative sign, the lower it is. Suspect a is $14$ and b is $10.$ If you compare $-14$ and $-10,$ the statement goes like this: $-14 \lt -10.$
Here is a diagram showing why the statement must also be true if $a$ and $b$ are both negative.
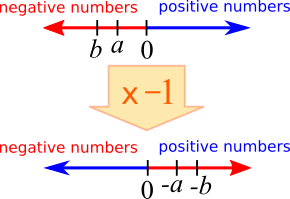
Here is a diagram showing why the statement must be true if $a$ is positive but $b$ is negative.

Terry and Miguel from International School of Krakow in Poland used a rule that comes from this idea. Terry wrote:
If you multiply or divide by a negative number, the direction of the inequality sign changes.
Yazan used an example to explain why statement 2 must be true:
Statement 2 ($a^2 + b^2 \ge 2ab$) is [correct] because two numbers squared can’t be [less than] the [product of] numbers by $2.$ Suppose $a$ is $7$ and $b$ is $3.$ $7^2$ is $49$ and $3^2$ squared is $9.$
$49+9=58,$ and $7\times3=21$ and $21x2=20,$ therefore, Statement 2 is [correct].
Terry and Miguel used algebra to show that statement 2 must always be true. This is Terry's work:
For the second argument, I began adding $-2ab$ to both sides, which made it $a^2-2ab+b^2\ge0.$ Knowing that $a^2-2ab+b^2$ can be expressed simply as $(a-b)^2,$ I changed the [inequality] into $(a-b)^2\ge0.$ The second argument is correct.
Naima from Bexley Grammar School and Vivek from Wilsons' School, both in the UK, gave examples to show that statement 3 is not necessarily true. Naima wrote:
We cannot say that statement 3 must be true. It will hold true if $c$ is positive - for example, if $a=4,b=2$ and $c=6,24\ge12.$
But if $c$ is negative, much like in statement 1 this will be reversed: if instead $c=-6,$ the expression will claim that $ac\ge bc,$ or $-24\ge-12,$ which is of course incorrect. So this statement will not be unconditionally true, despite $a$ being larger than $b.$
A single example is enough to show that a statement is not always true, so Naima and Vivek's examples are enough to show that it is definitely not true that statement 3 must be true. Miguel and Terry explained the same idea more generally. Miguel wrote:
Statement 3 is not always true as $c$ can be a negative number and therefore $bc$ would be greater than $ac.$
The Test of Mathematics for University Admission (or TMUA) is designed to give you the opportunity to demonstrate that you have the essential mathematical thinking and reasoning skills needed for a demanding undergraduate Mathematics or Mathematics-related course. There are several UK universities which encourage their applicants to sit TMUA, and a good performance may result in a reduced offer.
For more information about TMUA visit www.admissionstesting.org.
Teachers' Resources
This problem and the others in KS5 Proof shorts are great as lesson starters, warm downs or for stimulating discussion during a lesson. This problem helps students to understand what can be deduced from an inequality and the limited information about the values involved. It will encourage them to think clearly and carefully, testing intuitions with special cases and possible counterexamples.
