Turning to calculus
Get started with calculus by exploring the connections between the
sign of a curve and the sign of its gradient.
Age
16 to 18
Challenge level
The following curve turns once. It changes sign twice and the sign of its gradient changes once, giving rise to four distinct regions, as shown in the image below:
Image
What are the different possibilities of sign combination for a
curve which turns exactly once? How can you be sure you have found
them all? Give a clear explanation.
Which are the different possibilities of sign combination for a curve which turns exactly twice? How can you be sure you have found them all? Give a clear explanation.
Explore other numbers of turns and the curves which give rise to various numbers of regions.
It is not intended that you use algebra; simply experiment with sketches and focus on clear mathematical reasoning.
Further
extensions:
Once you have a good feel for the
setup, you might wish to think about these more tricky or general
questions:
1. Are there any curves which
always have the same sign for the function and gradient?
2. Are there any curves which
always have the opposite sign for the function and gradient?
3. Are there any impossible
combinations of sign?
4. How do zeros of the function
and zeros of the gradient enter into the analysis?
5. Find algebraic expressions
for any functions you use in this problem.
The gradients and signs of functions are strongly related for any nice, smooth curve which you can draw. To get into the problem you can sketch small line segments and ask yourself: how can these be smoothly joined together?
Image
Complications can arise for curves which turn suddenly or have gaps or become infinite at various points. Maybe you could think about creative ways to get from one place to the next.
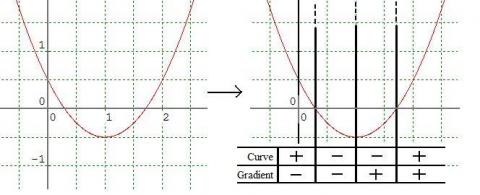
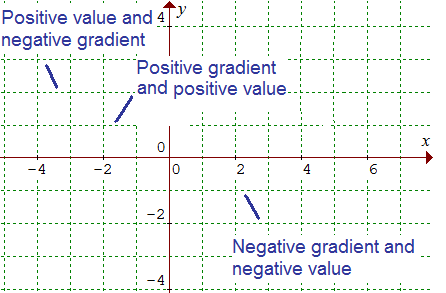
Why do this problem?
This problem is well suited for those who are about to begin to learn the concepts of calculus. It is easy to access, yet offers many insights into the relationships between functions and their derivatives. The language of calculus - change, derivative, turning points, maximum, minimum, curve, functions, equations, axes, zeros, continuity etc. - should naturally arise in the
exploration of this task and it should provide an natural framework on which to build the formality of calculus at a later date.
As with most NRICH tasks, this problem is low threshold high ceiling, so it also will prove an interesting exploration for the more sophisticated thinker.
Possible approach
You can use this task before the words 'turning points' and 'derivative' have been introduced to the students. Throughout the task encourage discussion and explanation of results either in pairs or to the class. An important aspect of the task is that students will discover, and struggle with describing, the concepts which will later become formalised with
calculus.
Start by suggesting that students draw a pair of coordinate axes and roughly sketch a curve which turns once (gradient changes sign). Ask them to locate the places on the x-axis where either the sign of their curve or the sign of its gradient changes.
Continue with a class discussion of which combinations of signs are possible for curves which turn once. Follow any interesting conjectures and spend time to unpick any confusion in definitions.
Elementary calculus concerns curves which are continuous, differentiable and have no asymptotes. However, perfectly reasonable curves exist which violate any or all of these properties (mod function, tan etc.). Furthermore, the concept of a function far transcends the notion of a curve (some functions don't have a curve) and there are nice curves (such as
circles) which are not functions. In trying to create their curves in this problem students will most likely introduce examples which are not functions, not continuous, not differentiable or have asymptotes. If this happens, great! Discussion concerning the sorts of curves which are appropriate for calculus will be a valuable learning point.
Once the concept is firmly understood, students can explore individually or in small groups the possibilities for curves which turn twice and then try systematically to find examples with 1 through to 6 possibilities for sign change.
Students might get involved with this task and start to experiment with curves or functions which break the conventional rules for functions. If this occurs, great! (as part of the subtlety with calculus concerns curves which are non-differentiable.)
Key questions
How can you sketch a curve where the sign of the gradient changes at some point?
What can you say about a curve which alternates in sign?
What happens to your results if you shift the axes up or down?
Can you think of any different 'types' of curves which have a particular combination of sign changes?
Possible extension
Skilled students can be encouraged to construct particularly interesting examples: pushing the boundaries of the problem is a good thing. For example, might there exist a curve with this combinations of signs?:
| Sign of function | + | + | + | - | - | - | + | + | + |
| Sign of function | + | - | + | - | + | - | + | - | + |
Why or why not?
Possible support
If people are struggling to start, sketch a curve with a few turns on the board and partition into regions of sign change collectively. Then suggest one person draws a curve and explains to the group the regions of sign change.
Students who are algebra-focussed might not perceive this to be 'maths'. Reassure them that mathematical reasoning is taking place and that constructing clear, precise examples and explanations is highly mathematical and will provide a very solid foundation for the algebraic calculus which will follow.