Sprouts Explained
Breaking the Equation 'empirical Argument = Proof '
This article stems from research on the teaching of proof and offers guidance on how to move learners from focussing on experimental arguments to mathematical arguments and deductive reasoning.
Air Nets
Impossible Sandwiches
Geometry and Gravity 2
The bridges of Konigsberg
Investigate how networks can be used to solve a problem for the 18th Century inhabitants of Konigsberg.
Yih or Luk tsut k'i or Three Men's Morris
Some puzzles requiring no knowledge of knot theory, just a careful inspection of the patterns. A glimpse of the classification of knots and a little about prime knots, crossing numbers and knot arithmetic.
What Does It All Add Up To?
To Prove or Not to Prove
Some Circuits in Graph or Network Theory
An Introduction to Proof by Contradiction
Proof: a Brief Historical Survey

Binomial Coefficients
An introduction to the binomial coefficient, and exploration of some of the formulae it satisfies.
A Knight's Journey
Picturing Pythagorean triples
This article discusses how every Pythagorean triple (a, b, c) can be illustrated by a square and an L shape within another square. You are invited to find some triples for yourself.
Which Spinners?
Can you work out which spinners were used to generate the frequency charts?
Iffy Logic
Can you rearrange the cards to make a series of correct mathematical statements?
Summing Geometric Progressions
Watch the video to see how to sum the sequence. Can you adapt the method to sum other sequences?
There's a Limit
Perception Versus Reality
Infographics are a powerful way of communicating statistical information. Can you come up with your own?
Mega Quadratic Equations
What do you get when you raise a quadratic to the power of a quadratic?
Network Trees
Unit Interval
Common Divisor
Can you find out what numbers divide these expressions? Can you prove that they are always divisors?
Dalmatians
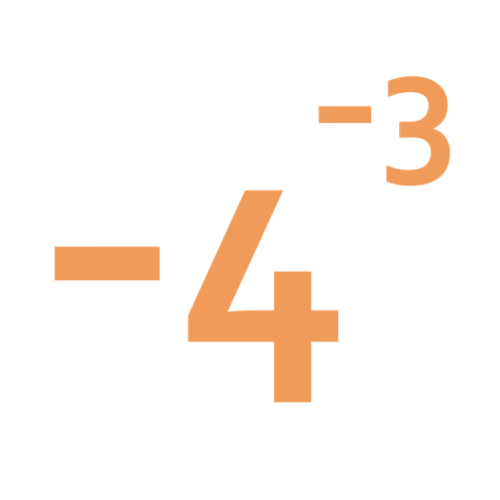
Negative Powers
What does this number mean? Which order of 1, 2, 3 and 4 makes the highest value? Which makes the lowest?
Always Perfect
Show that if you add 1 to the product of four consecutive numbers the answer is ALWAYS a perfect square.
Calculating with Cosines
If I tell you two sides of a right-angled triangle, you can easily work out the third. But what if the angle between the two sides is not a right angle?
Kite in a Square
Can you make sense of the three methods to work out what fraction of the total area is shaded?
Sixational
Impossible Sums
Which numbers cannot be written as the sum of two or more consecutive numbers?
Always Two
Find all the triples of numbers a, b, c such that each one of them plus the product of the other two is always 2.
Curve Fitter
This problem challenges you to find cubic equations which satisfy different conditions.

Quad in Quad
Join the midpoints of a quadrilateral to get a new quadrilateral. What is special about it?
Difference of Odd Squares
$40$ can be written as $7^2 - 3^2.$ Which other numbers can be written as the difference of squares of odd numbers?
Back Fitter
10 graphs of experimental data are given. Can you use a spreadsheet to find algebraic graphs which match them closely, and thus discover the formulae most likely to govern the underlying processes?
Proof Sorter - Quadratic Equation
The converse of Pythagoras
Can you prove that triangles are right-angled when $a^2+b^2=c^2$?
Iff
Take a triangular number, multiply it by 8 and add 1. What is special about your answer? Can you prove it?
Pent

A Long Time at the Till
Try to solve this very difficult problem and then study our two suggested solutions. How would you use your knowledge to try to solve variants on the original problem?
Leonardo's Problem
Sums of Squares and Sums of Cubes
Transitivity
Modulus Arithmetic and a Solution to Dirisibly Yours
Continued fractions II
In this article we show that every whole number can be written as a continued fraction of the form k/(1+k/(1+k/...)).
Fractional calculus III
Fractional calculus is a generalisation of ordinary calculus where you can differentiate n times when n is not a whole number.
Sperner's Lemma
Euler's Formula and Topology
A Computer Program to Find Magic Squares
An Alphanumeric
Powerful Properties
The Kth Sum of N Numbers
Euclid's algorithm II
We continue the discussion given in Euclid's Algorithm I, and here we shall discover when an equation of the form ax+by=c has no solutions, and when it has infinitely many solutions.
An Introduction to Number Theory
An introduction to some beautiful results in Number Theory.
On the Importance of Pedantry
A introduction to how patterns can be deceiving, and what is and is not a proof.
Telescoping Functions
Where Do We Get Our Feet Wet?
Why Stop at Three by One
Beautiful mathematics. Two 18 year old students gave eight different proofs of one result then generalised it from the 3 by 1 case to the n by 1 case and proved the general result.
Modulus Arithmetic and a Solution to Differences
Patterns of Inflection
Find the relationship between the locations of points of inflection, maxima and minima of functions.
Polynomial Relations
Three by One
There are many different methods to solve this geometrical problem - how many can you find?
Big and Small Numbers in Physics - Group Task
Stonehenge
Archimedes Numerical Roots
How did Archimedes calculate the lengths of the sides of the polygons which needed him to be able to calculate square roots?
More Dicey Decisions
Code to Zero
Stats Statements
Are these statistical statements sometimes, always or never true? Or it is impossible to say?
Fibonacci Factors
Without Calculus
Pair Squares
Diverging
Flexi Quad Tan
Pythagorean Golden Means
Direct Logic
Can you work through these direct proofs, using our interactive proof sorters?
Flexi Quads
A quadrilateral changes shape with the edge lengths constant. Show the scalar product of the diagonals is constant. If the diagonals are perpendicular in one position are they always perpendicular?
Tetra Inequalities
Can you prove that in every tetrahedron there is a vertex where the three edges meeting at that vertex have lengths which could be the sides of a triangle?
Three Ways
Big, Bigger, Biggest
Which is the biggest and which the smallest of $2000^{2002}, 2001^{2001} \text{and } 2002^{2000}$?
Proving the Laws of Logarithms
Here you have an opportunity to explore the proofs of the laws of logarithms.
Staircase
Integration Matcher
Can you match the charts of these functions to the charts of their integrals?
Prime AP
What can you say about the common difference of an AP where every term is prime?
Prime Sequences
Quadratic Harmony
Dangerous Driver?
Was it possible that this dangerous driving penalty was issued in error?
Adding Odd Numbers (part 2)
Can you use Proof by Induction to establish what will happen when you add more and more odd numbers?
