Why Stop at Three by One
In this article Alex and Neil from Madras College give a generalisation of the Three By One problem. See also the article by the same authors, 8 Methods for 'Three by One' which, as the title suggests, brilliantly solves the same problem using 8 different topics in mathematics thus exemplifying the unity of the subject.
Image
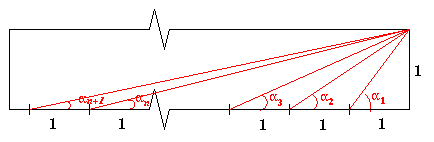
Given a rectangle of dimensions 1 by $n$, for each angle, $\alpha_m$ where $m$ is a positive integer, are there two other angles $\alpha_p$ and $\alpha_q$ whose sum is equal to $\alpha_m$?
Now \begin{eqnarray} \alpha_m & = & \tan^{-1}(1/m)\\ \alpha_p & = & \tan^{-1}(1/p)\\ \alpha_q & = & \tan^{-1}(1/q) \end{eqnarray}.
Using an exhaustive search for each $m$ from 1 to 12 the $(p,q)$ which satisfy this are:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
| ( p , q ) pairs | (2,3) | (3,7) | (4,13) | (5,21) | (6,31) | (7,43) | (8,57) | (9,73) | (10,91) | (11,111) | (12,133) | (13,157) |
| (3,2) | (5,8) | (7,18) | (9,32) | (13,21) | (11,50) | (13,72) | ||||||
| (12,17) |
Now, using the tan angle sum formula: \begin{eqnarray} \alpha_m = \alpha_p + \alpha_q & \Rightarrow &\tan^{-1}(1/m)= \tan^{-1}(1/p)+ \tan^{-1}(1/q)\\ & \Rightarrow &\tan(\tan^{-1}(1/m))= \tan(\tan^{-1}(1/p)+ \tan^{-1}(1/q))\\ & \Rightarrow & {1\over m} = {(1/p)+ (1/q)\over 1 - (1/pq)}\\ & \Rightarrow & {1\over m} = {p + q \over pq - 1}\\ & \Rightarrow & q = {mp + 1 \over p - m} \end{eqnarray} If $p$ and $q$ satisfy this diophantine equation then these will be solutions to the above question for $\alpha_m$.
Conjecture 1:
For all $m$ there exists at least one solution where $p = m + 1$.
Proof:
To find a solution, use: $$q = {mp+1\over p - m}.$$ When $p = m+1$ $$q = m^2+ m +1.$$ Since $p$ and $q$ are integers there are two angles in the extended diagram which add up to $\alpha_m$.
