How Many Solutions?
Find all the solutions to the this equation.
Age
16 to 18
Challenge level
Problem
Find all solutions to
Getting Started
You might find some roots by trial and error but can you be sure
you have found them all?
Student Solutions
This is a 'quickie'.
Ling Xiang Ning of Raffles Institution in Singapore, found two solutions, and after trying some more values of x, decided that there would be no more because:
"The graphs of $y = x$ and $y = (\sqrt {2})^x$ cut at exactly two points $(2, 2)$ and $(4, 4)$ so there are exactly two solutions."
Vassil from Lawnswood High School in
Leeds, used a different graph to convince himself that there were
no more solutions.
First of all, he rearranged the equation:
$$ \eqalign { x &=&
(\sqrt{2})^x \\ \sqrt[x]{x} &=& \sqrt{2} }$$ (taking the
$x^{th}$ root)
$$ \eqalign { (\sqrt[x]{x})^2
&=& 2 \\ x^{\frac{2}{x}} &=& 2 } $$
(squaring).
Next he calculated values of $x^{\frac{2}{x}}$ from $1$ to $8$, and plotted this graph:
Image
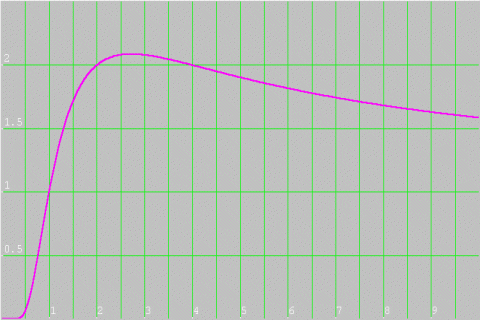
Vassil commented that by looking at the original equation we could rule out negative values of $x$, and that the values in the graph decline after $x=4$. The justification for the decline is that we are calculating smaller and smaller powers. However, you may not be convinced, as the number we are finding powers of is getting bigger. Are you sure that curve isn't going to go up again further along?
The use of a graph to justify there being only 2 solutions was a good idea.
Clearly $x=0$ is not a solution and there are no negative
solutions because the right hand side is positive. We have found 2
solutions $x=2$ and $x=4$ and we have to show that there are no
other solutions.
Consider the function $f(x) = (\sqrt 2)^x = exp(x\ln \sqrt
2)$. Differentiating the function gives: $$\frac{df}{dx} = (ln
\sqrt 2)\times exp(x\ln \sqrt 2)$$ and $$\frac{d^2f}{dx^2} = (ln
\sqrt 2)^2\times exp(x\ln \sqrt 2)> 0.$$ So the graph of f is
convex (the first derivative, or gradient, is always increasing) so
the graph of $y=f(x)$ meets $y=x$ in at most 2 points. So $2$ and
$4$ are the only solutions.