Magic W wrap up
Prove that you cannot form a Magic W with a total of 12 or less or with a with a total of 18 or more.
Problem
To make a Magic W you have to put the numbers 1, 2, ...,9, one in each circle, so that each row of three numbers has the same total. Experiment to find as many different magic totals as you can using the interactivity from the Magic W problem.
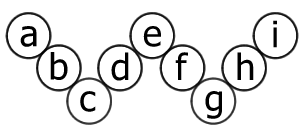
Prove that if you have a Magic W and you replace each of the numbers by 10 minus that number then the new W is also magic. What will its magic total be?
Prove that you cannot form a Magic W with a total of 12 or less. Also prove that you cannot form a Magic W with a total of 18 or more.
Getting Started
See the solution to the Magic W problem from May 2003
Student Solutions
Judy sent us the following solution:
Suppose that we have a labelling with magic total $T$ that looks like this:
$A\quad\quad E\quad\quad I$
$\ B\quad D\quad F\quad H$
$\quad C\quad \quad G\quad $
Then we can replace each entry $x$ by $10-x$ and get another labelling (because if $x$ is one of 1, 2, \ldots, 9, then $10-x$ will also be). Also, this label will have magic total $30-T$, because instead of adding up $A+B+C$, for example, we'll add up $10-A+10-B+10-C=30-T$, and all of the sums will be the same. So if we have a labelling with magic total $T$, then we certainly have one with magic total $30-T$.
Using the solution to the Magic W problem, we know that there is 1 magic labelling for $T=13$, and there are 5 for $T=14$. So (using what we worked out above) there's also one for $T=17$ and 5 for $T=16$. (There can't be any more for $T=17$, for example, because any labelling of $T=17$ is also one of $T=13$.)
When do magic labellings exist? Well, again using the ideas from the solution to the Magic W problem, we must have $C+E+G+45=4T$. But $C+E+G\geq 6$, so $4T\geq 45+6=51$, so $T\geq 13$. Also, $C+E+G\leq 24$, so $4T\leq 45+24=69$ so $T\leq 17$. So we only need to check whether there are any magic labellings for $T=15$. Suppose that there is one. Then we have $C+D+E=15$, and also $C+E+G=4\times 15-45=15$, so $D=G$. But that's not allowed, so there are no labellings of $T=15$.
To summarise, there are magic labellings for $T=13, 14, 16$ and $17$ (and no others), and there are $1+5+5+1=12$ magic labellings.
