IFFY triangles
Can you prove these triangle theorems both ways?
Problem
Here are four triangle facts for you to prove, in two groups of two.
1(a)
Let $ABC$ be a triangle with angles $A$, $B$ and $C$ where $A \le B \le C$ and $A$, $B$ and $C$ form an arithmetic progression.
Prove that $B=60^{\circ}$.
1(b)
$XYZ$ is a triangle with angles $X$, $Y$ and $Z$ and we have $Y = 60^{\circ}$.
Prove that $X$, $Y$ and $Z$ form an arithmetic progression.
2(a)
$PQR$ is a triangle with length $PQ$ equal to length $QR$.
Prove that angles $P$ and $R$ are equal.
2(b)
$KLM$ is a triangle with equal angles $K$ and $M$.
Prove that the lengths $KL$ and $LM$ are equal.
Can you write each pair as a single "If and only if" statement?
Getting Started
An arithmetic progression is where the terms of a sequence are increasing (or decreasing) by the same amount each time. Here are two examples:
- $50, 60, 70$
- $66, 62, 58$
In the first case the numbers are increasing by $10$ each time and in the second they are decreasing by $4$ each time. Only one of the two sets of numbers above can represent the angles in a triangle.
For the second pair of problems, a diagram might be useful. You might find it helpful to add an extra line to your diagram and to think about congruent triangles. Be careful that you don't assume things that need to be proved!
Student Solutions
Nayanika from The Tiffin Girls' School and Ben from Thomas Hardye, both in the UK, both proved the first pair of statements, and an anonymous solution combined the two statements into a single 'if and only if' statement.
This is Nayanika's proof for statement 1a (if $A,B$ and $C$ are in an arithmetic progression, then $B=60^\circ$):
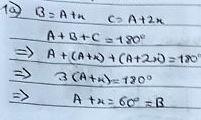
This is Ben's proof for statement 1b (if $Y=60^\circ,$ then $X, Y$ and $Z$ are in an arithmetic progression):

Ben's proof is good, but the final statement is actually the wrong way around. Ben started by assuming that $Y=60,$ and showed that whenever $Y=60,$ $X,Y$ and $Z$ form an arithmetic progression. This is written as $$Y=60\Rightarrow X,Y,Z\text{ form an arithmetic progression}$$
An anonymous solution combined this pair of statements into a single 'if and only if' statement:
Therefore, $ABC$ is a triangle with angles $A,B$ and $C$ where $A\lt B\lt C$ $$A,B,C \text{ form an arithmetic progression}\iff B=60$$
Ben and Nayanika both sent in proofs for the second pair of statements, and the anonymous solution combined them into a single 'if and only if' statement.
Ben proved statement 2a (that in a triangle $PQR,$ if the lengths $PQ$ and $QR$ are equal, then angles $P$ and $R$ are equal):

To confirm that the perpendicular bisector to side $PR$ really does pass through $Q$ and $S,$ note that $Q$ and $S$ are both equidistant from $P$ and $R.$
Nayanika proved statement 2b (that in a triangle $KLM,$ if angles $K$ and $M$ are equal, then lengths $KL$ and $LM$ are equal) using congruence:

Ben proved statement 2b using trigonometry:

Once again, the anonymous solution combined the two statements into one single 'if and only if' statement:
Therefore, PQR is a triangle $$PQ = QR \iff \hat{P} = \hat{Q}$$
Teachers' Resources
This problem encourages students to think about the directions of implication ("if" and "only if"). They can also be introduced to the $\implies$, $\Longleftarrow$, and $\iff$ notation. Question $1$ uses the idea of an arithmetic progression, and question $2$ can be solved by using congruent triangles. The results of question $2$ should be familar to students, but they might not have met a proof of this result before.
Here are some statements that can be used to introduce "if" and "only if" (or "implies" and "is implied by") notation. In each case students should discuss which are correct and which are not correct.
- Tiddles is a cat $\Longrightarrow$ Tiddles is not a horse
Tiddles is a cat $\Longleftarrow$ Tiddles is not a horse
- $n$ is odd $\Longrightarrow$ $n^2$ is odd
$n$ is odd $\Longleftarrow$ $n^2$ is odd
- $x^2=1$ $\Longrightarrow$ $x=1$
$x^2=1$ $\Longleftarrow$ $x=1$
- $n$ is a multiple of $4$ $\Longrightarrow$ $n^2$ is a multiple of $4$
$n$ is a multiple of $4$ $\Longleftarrow$ $n^2$ is a multiple of $4$
For the second example both directions are true so we can write "$n$ is odd $\iff$ $n^2$ is odd". Students can be challenged to come up with some examples of their own, and there are more examples in the problem Iffy Logic.
Possible extension
Students might like to consider Euclid's "Pons Asinorum" (bridge of donkeys) proof that a triangle with two equal sides has two equal angles. In this proof, the congruent triangle condition $SSS$ cannot be assumed (as Euclid had not proved this at this point!). This proof is explored in question 4 of this STEP Support Programme Assignment.
