Sliding game
Fractions and coins game
Seeing squares for two
Phiddlywinks
Tessellation interactivity
Tangram browser
Interactive balance
Less is more
Number lines in disguise
How long does it take?
Four-digit targets
First connect three
Square tangram
Mathdoku
Your number is...
Matching fractions, decimals and percentages
Multiplication tables - matching cards
Flip flop - matching cards
Colour in the square
4 dom
Tea cups
Mystery matrix
Largest even
Unravelling sequences
Triangle in a square
An easy way to multiply by 10?
Dotty circle
Triangle pin-down
Arrangements
A square of numbers
1, 2, 3 magic square
Missing multipliers
Junior frogs
Latin lilies
Rod ratios
Cuisenaire squares
Rod fractions
Board block challenge for two
More transformations on a pegboard
Geoboards
Flip
Difference
Red or black spinner
Ducking and dividing
Your vessel, the Starship Diophantus, has become damaged in deep space. Can you use your knowledge of times tables and some lightning reflexes to survive?
First connect three for two
First Connect Three game for an adult and child. Use the dice numbers and either addition or subtraction to get three numbers in a straight line.
Got it
A game for two people, or play online. Given a target number, say 23, and a range of numbers to choose from, say 1-4, players take it in turns to add to the running total to hit their target.
Twice as big?
Investigate how the four L-shapes fit together to make an enlarged L-shape. You could explore this idea with other shapes too.
Carroll diagrams
Use the interactivities to fill in these Carroll diagrams. How do you know where to place the numbers?
Growing garlic
Ben and his mum are planting garlic. Can you find out how many cloves of garlic they might have had?
The remainders game
Play this game and see if you can figure out the computer's chosen number.
Matching fractions
Can you find different ways of showing the same fraction? Try this matching game and see.
A puzzling cube
Here are the six faces of a cube - in no particular order. Here are three views of the cube. Can you deduce where the faces are in relation to each other and record them on the net of this cube?
Board block challenge
Choose the size of your pegboard and the shapes you can make. Can you work out the strategies needed to block your opponent?
Seeing parallelograms
Players take it in turns to choose a dot on the grid. The winner is the first to have four dots that can be joined to form a parallelogram.
Seeing rhombuses
Players take it in turns to choose a dot on the grid. The winner is the first to have four dots that can be joined to form a rhombus.
Quadrilaterals
How many DIFFERENT quadrilaterals can be made by joining the dots on the 8-point circle?
Remainders
I'm thinking of a number. My number is both a multiple of 5 and a multiple of 6. What could my number be?
Celebrate 25 years of NRICH
To celebrate NRICH's 25th birthday, why not play this special version of our classic game, Got It? Can you devise a strategy so that you will always win?
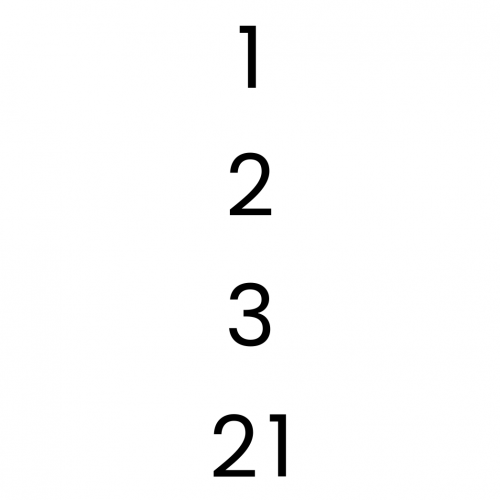
Factor lines
Arrange the four number cards on the grid, according to the rules, to make a diagonal, vertical or horizontal line.

World of Tan 2 - Little Ming
Can you fit the tangram pieces into the outline of Little Ming?


World of Tan 4 - Monday morning
Can you fit the tangram pieces into the outlines of Wai Ping, Wu Ming and Chi Wing?



World of Tan 7 - Golden goose
Can you fit the tangram pieces into the outline of the plaque design?

World of Tan 8 - Sports car
Can you fit the tangram pieces into the outline of the sports car?

World of Tan 9 - Animals
Can you fit the tangram pieces into the outlines of the camel and giraffe?

World of Tan 13 - A storm in a tea cup
Can you fit the tangram pieces into the outlines of the convex shapes?

World of Tan 12 - All in a fluff
Can you fit the tangram pieces into the outlines of the rabbits?

World of Tan 11 - The past, present and future
Can you fit the tangram pieces into the outlines of the telescope and microscope?

World of Tan 10 - Butterflies
Can you fit the tangram pieces into the outline of the butterfly?

World of Tan 14 - Celebrations
Can you fit the tangram pieces into the outlines of Little Ming and Little Fung dancing?

World of Tan 15 - Millennia
Can you fit the tangram pieces into the outlines of the numbers?



World of Tan 18 - Soup
Can you fit the tangram pieces into the outlines of Mah Ling and Chi Wing?

World of Tan 19 - A circular problem
Can you fit the tangram pieces into the outline of this teacup?


World of Tan 21 - Almost there now
Can you fit the tangram pieces into the outlines of the lobster, yacht and cyclist?

World of Tan 22 - An appealing stroll
Can you fit the tangram pieces into the outline of the child walking home from school?

World of Tan 23 - Transform this into that
Can you fit the tangram pieces into these outlines?


World of Tan 25 - Pentominoes
Can you fit the tangram pieces into the outlines of the people?

World of Tan 26 - Old chestnut
Can you fit the tangram pieces into the outline of the brazier for roasting chestnuts?

World of Tan 27 - Sharing
Can you fit the tangram pieces into the outline of Little Fung at the table?

World of Tan 28 - Concentrating on coordinates
Can you fit the tangram pieces into the outline of the playing piece?

World of Tan 29 - The telephone
Can you fit the tangram pieces into the outline of the telephone?

World of Tan 30 - Logical thinking
Can you logically construct these silhouettes using the tangram pieces?
Older upper primary Flash-based interactives
The activities below are older resources which require Flash in order to run.No results found
