Square tangram
Problem
A set of shapes has five pieces:
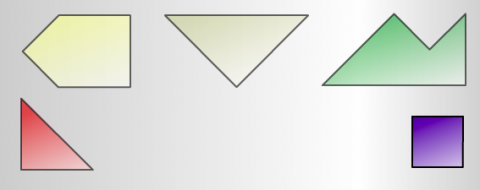
Can you make a square using four of the pieces?
You may like to use the interactivity below to try out your ideas, or download this sheet with two sets of pieces for printing and cutting.
Now, can you make a square using all five pieces?
Now, add another set of five pieces (so now there are ten). Can you make a square with all of them?
Printable NRICH Roadshow resource.
Getting Started
For making a square using four pieces, take out the little square.
Student Solutions
This is much more tricky than it looks, isn't it?! Well done to those of you who managed to make a square using four or five pieces. Callum from Brookside Primary, Becky from Holy Cross C of E School, Jonah from Great Wilbraham Primary and Max from Eastwood Primary made a square with four pieces. Here is Becky's solution which correctly leaves out the small square:
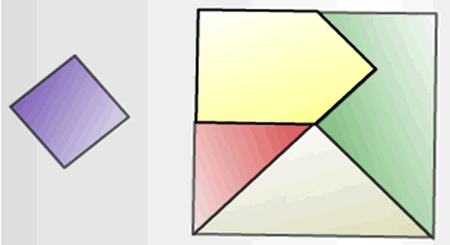
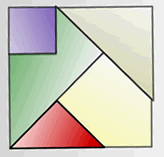
Dafydd, also from Holy Cross, and Rowley from Culford Primary solved the five-piece challenge. This is Rowley's image:
Mel from Christ Church Grammar, Rowley from Culford Primary, Eleanor from Great Wilbraham Primary, Callum from Castle Carrock Primary and Shiv from Sanskaar Valley, Bhopal in India, all sent in solutions to the ten-piece challenge. In fact, between them they managed to come up with four different ways of solving it! Well done everyone!
A while later, we received another solution from Hannah from Diocesan School for Girls, Auckland, New Zealand. With the help of her older brother, Hannah came up with this additional solution to the ten-piece problem:
Thank you for sending this in, Hannah.
Teachers' Resources
Square Tangram
A set of shapes has five pieces:
Can you make a square using four of the pieces?
You may like to use the interactivity below to try out your ideas, or download this sheet with two sets of pieces for printing and cutting.
Now, can you make a square using all five pieces?
Now, add another set of five pieces (so now there are ten). Can you make a square with all of them?
Printable NRICH Roadshow resource.
Why do this problem?
This tangram is a challenging context in which to remind pupils of the properties of squares. Tangrams offer a fantastic starting point for nurturing flexibility in the primary classroom. To find out more about developing mathematical flexibility through geometry, take a look at this article.
Possible approach
You could display the interactivity on the board and start by asking children to look at the image on the left (of the tangram pieces). Invite them to consider what they see and what they might like to ask. Give them time to think on their own, then talk to a partner about their 'noticings'. Encourage some pairs to share their observations and questions with the whole group. Try to take a step back and allow the class to respond to the comments and questions themselves, rather than you validating all contributions. Some children might talk about the different shapes they can see (and colours). Encourage use of mathematical vocabulary where appropriate. Build on their thoughts to introduce the idea of a tangram and the task itself.
You can then set the class off in pairs on the challenges. After some time, invite them to offer 'hints' for the rest of the group, without giving away a solution. Perhaps they can offer advice about what they are finding helpful to focus on as they tackle the challenges, perhaps they can suggest a starting point for one of the squares... It is important that children become more confident at simply 'having a go' and playing with their ideas to begin with, rather than feeling that they need to know the 'right' way to do it from the start. You might like to model this trial and improvement approach, emphasising that we can learn a lot from what doesn't work.
These challenges are not straightforward and learners are likely to get stuck. Talk about this with the class. How does it feel to be stuck? How are they trying to get unstuck? How does it feel when they make a breakthrough? You can stop the class as appropriate to share experiences.
The completed squares could make a lovely classroom display, accompanied by some brief notes written by the class, focusing on how they went about finding solutions.
Key questions
What have you tried so far?
Is there a way to tweak what you have done, rather than starting from scratch again?
How will you remember what you have tried?
Possible extension
Learners could create 'clue cards' to offer support to their peers, without giving away the solution.
Possible support
Encouraging a playful approach to this task will help make it accessible to all learners.