A Puzzling Cube
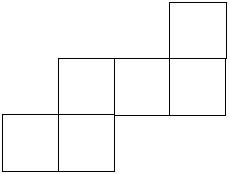
Here are the six faces of a cube - in no particular order. Here are three views of the cube. Can you deduce where the faces are in relation to each other and record them on the net of this cube?
Problem
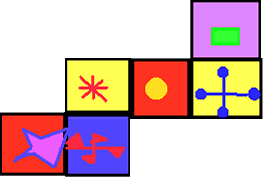
Here are the six faces of a cube - in no particular order:
For accessibility: The first face of the cube is red and has a purple star. The second face of the cube is yellow and has 2 blue lines on it. The third face is blue and has 2 red lines on it. The fourth face is purple and has a green square on it. The fifth face is green and has a red star on it. The sixth face is red and has a yellow circle on it.
Here are three views of the cube:
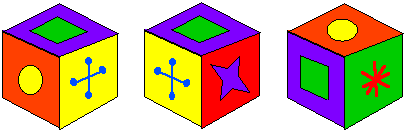
For accessibility: The 3 cubes show the top face and two side faces that are next to each other. The first cube shows the purple face with the green square as the top face, the red face with the yellow circle as the left side face, and the yellow face with 2 blue lines as the right side face. The second cube shows the purple face with a green square as the top face, the yellow face with 2 blue lines as the left side face, and the red face with the purple star as the right side face. The third cube shows the red face with a yellow circle face as the top face, the purple face with the green square as the left side face and the green face with the red star as the right side face.
Can you deduce where the faces are in relation to each other and record them on the net of this cube?
Getting Started
You could print out this sheet or draw the faces of the cube to help you. Cut out each one separately and move them around until they fit the views of the cube given. You might need some sticky tape!
Try concentrating on two the faces which are next to each other to start with. Which other face is near them?
Student Solutions
| This problem is a little more difficult than it looks. However, we had many correct reponses. Although there is only one cube, its net can be drawn in different ways. Bronya from Tattingstone School describes how she went about solving the puzzle: | |
First I drew the first three faces of the cube as a net: | Image
|
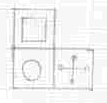
| Then I looked at the next 3 faces. I saw that the 4 pointed star was next to one of the shapes I had put down. I added it onto the net: | Image
|
| On the third picture of the cube the square was on the side and the circle on the top. If the circle was on the side the other symbol would be at the side. I put the shape down on my net: | Image
|
| There was only one shape left so it had to go at the bottom. I put this down on my net: | Image
|
| To check, I made one of my own to see if it would fit with all the pictures. It did! | Image
|
| Kyle and Allyssa from Oakwood Junior School both tried out their ideas on paper before drawing these nets: | |
Image
| Image
|
| Tom Neill sent in another net of the same cube which was also sent by Angus from Maldon Court Preparatory School: | |
Image
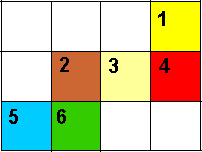
| 1 is the cross on the yellow background 2 is the circle on the orange background 3 is the flag cross on the blue background 4 is the star on the red background 5 is the rectangle on the purple background 6 is the star on the green background |
| Philip who goes to Arnold School in Lancashire said, "I looked at it from different views to find the solution." Here is Philip's net: | |
Image
| |
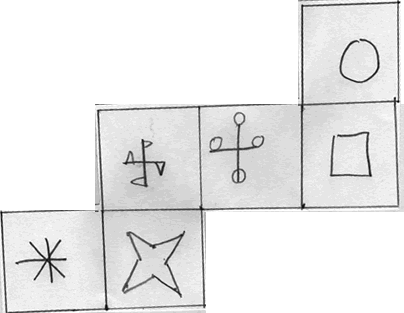
| Martha, also from Tattingstone, made up a cube from the net before deciding which face the shapes were on. Here is her work: | |
Image
| |
Rhys from St Mary's in Templemore, Co. Tipperary, Ireland wrote to tell us: Image
| |
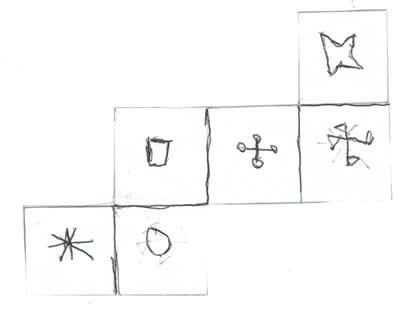
Teachers' Resources
A Puzzling Cube
Here are the six faces of a cube - in no particular order:
Here are three views of the cube:
Can you deduce where the faces are in relation to each other and record them on the net of this cube?
Why do this problem?
This problem is a little more difficult than it looks. It requires children to visualise the adjoining faces of the cube and transfer them to a net of the cube.
Possible approach
You could start by showing the group the problem on an interactive whiteboard. Once you have discussed what needs to be done, children could work in pairs so that they are able to talk through their ideas with a partner. If tablets or computers are available, they could use the interactivity to keep track of their thinking. In addition, they could use a print-out of this sheet or draw the faces of the cube for themselves. Some children might request cube-shaped objects, such as large dice, to help them work on the task. Scissors, sticky tape and blutak would also be useful!
As you walk around the room, look out for different ways of approaching the task. Some children may want to construct the cube from individual squares, then 'undo' the construction to create the net. Others may prefer to visualise the arrangement of faces and transfer them straight on to the net. (Learners could use a different arrangement which can be folded into a cube, not necessarily just the conventional cross-shaped net given on the sheet.)
At the end of the lesson, it would be worth inviting some pairs to talk through their approach. Do all the resulting nets look the same? Why or why not? The class' nets and cubes would make a great display, along with a copy of the challenge itself.
Key questions
Why do you think these two faces are next to each other on the cube?
Look at these two faces. Which other one goes near them?
Possible extension
Some learners can be challenged to make the net of the octahedron from this sheet.
Possible support
Suggest making a net from this sheet and leaving it so it can be folded and unfolded. Then draw or paste on the faces one by one. If 'Polydron' squares are available the cube can be built up using the pieces from this sheet.