Rotations

problem

Cubic Spin

Age

16 to 18

Challenge level

2 out of 3

Prove that the graph of f(x) = x^3 - 6x^2 +9x +1 has rotational symmetry. Do graphs of all cubics have rotational symmetry?
problem

Footprints

Age

16 to 18

Challenge level

2 out of 3

Make a footprint pattern using only reflections.
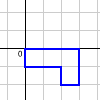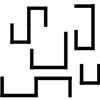problem

Shape Mapping

Age

7 to 11

Challenge level

2 out of 3

What is the relationship between these first two shapes? Which shape relates to the third one in the same way? Can you explain why?
problem

Interpenetrating Solids

Age

16 to 18

Challenge level

2 out of 3

This problem provides training in visualisation and representation of 3D shapes. You will need to imagine rotating cubes, squashing cubes and even superimposing cubes!
problem

Illusion

Age

11 to 16

Challenge level

3 out of 3

A security camera, taking pictures each half a second, films a cyclist going by. In the film, the cyclist appears to go forward while the wheels appear to go backwards. Why?
problem

In a Spin

Age

14 to 16

Challenge level

3 out of 3

What is the volume of the solid formed by rotating this right angled triangle about the hypotenuse?
problem

Symmetric Trace

Age

14 to 16

Challenge level

3 out of 3

Points off a rolling wheel make traces. What makes those traces have symmetry?
problem

Star Find

Age

5 to 7

Challenge level

2 out of 3

Can you see which tile is the odd one out in this design? Using the basic tile, can you make a repeating pattern to decorate our wall?
problem

Animated Triangles

Age

5 to 7

Challenge level

2 out of 3

Watch this "Notes on a Triangle" film. Can you recreate parts of the film using cut-out triangles?
problem

Same Shapes

Age

5 to 7

Challenge level

3 out of 3

How can these shapes be cut in half to make two shapes the same shape and size? Can you find more than one way to do it?