Inequalities
-

-

-
 problemFavourite
problemFavouriteWhich is bigger?
Which is bigger, n+10 or 2n+3? Can you find a good method of answering similar questions?
-
 problemFavourite
problemFavouriteTet-trouble
Is it possible to have a tetrahedron whose six edges have lengths 10, 20, 30, 40, 50 and 60 units?
-
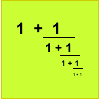 problem
problemNot continued fractions
Which rational numbers cannot be written in the form x + 1/(y + 1/z) where x, y and z are integers? -
 problem
problemBig, bigger, biggest
Which is the biggest and which the smallest of $2000^{2002}, 2001^{2001} \text{and } 2002^{2000}$?
-
 problem
problemTetra inequalities
Can you prove that in every tetrahedron there is a vertex where the three edges meeting at that vertex have lengths which could be the sides of a triangle?
-

-

-
 problemFavourite
problemFavouriteGiants
Which is the bigger, 9^10 or 10^9 ? Which is the bigger, 99^100 or 100^99 ?
