Inequalities
-

-

-
 problemFavourite
problemFavouriteSquare mean
Is the mean of the squares of two numbers greater than, or less than, the square of their means? -
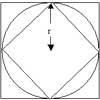 problemFavourite
problemFavouriteApproximating pi
By inscribing a circle in a square and then a square in a circle find an approximation to pi. By using a hexagon, can you improve on the approximation? -
 problem
problemFracmax
Find the maximum value of 1/p + 1/q + 1/r where this sum is less than 1 and p, q, and r are positive integers. -
 problemFavourite
problemFavouriteSquareness
The family of graphs of x^n + y^n =1 (for even n) includes the circle. Why do the graphs look more and more square as n increases? -

-
 problem
problemInequalities
A bag contains 12 marbles. There are more red than green but green and blue together exceed the reds. The total of yellow and green marbles is more than the total of red and blue. How many of each colour there are in the bag?
-
 problem
problemPlutarch's boxes
According to Plutarch, the Greeks found all the rectangles with integer sides, whose areas are equal to their perimeters. Can you find them? What rectangular boxes, with integer sides, have their surface areas equal to their volumes?
-
 problemFavourite
problemFavouriteWhich is cheaper?
When I park my car in Mathstown, there are two car parks to choose from. Can you help me to decide which one to use?
