Biggest Enclosure
Three fences of different lengths form three sides of an enclosure. What arrangement maximises the area?
Problem
Three fences of lengths $p$, $q$ and $r$ with $p< q< r$ are arranged to form three sides $AB$, $BC$ and $CD$ of a field $ABCD$ with right angles at $B$ and $C$.
Image
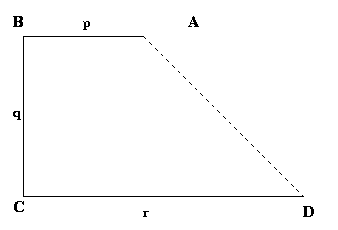
The diagram shows one possibility but the fences can be exchanged to make different enclosures.
The enclosure is completed by joining $A$ and $D$.
How should the rods be arranged to make the area of the enclosure as big as possible?
Student Solutions
Image

|
Shaun of Nottingham High School and also Ben and Thomas sent in good solutions to this problem. Here is Shaun's solution.
There are three possibilities we must consider, in each one the 'middle' fence (vertical in the diagram ) is one of $p$, $q$ or $r$. Interchanging the horizontal fences either side makes no difference to the area of the shape, it is just being flipped vertically. Remember the area of a trapezium can be expressed as ${1\over 2}(a+b)h$, where $a$ and $b$ are parallel sides, and $h$ the distance between them. |
This means we can express the areas of the three possible shapes as:
$$\frac {1}{2}(p+q)r, \frac {1}{2}(q+r)p, \frac {1}{2}(r+p)q.$$
Let's compare the first two. As $qr> qp$ we have $qr + pr > qp + pr$ and so
$${1\over 2}(p+q)r > {1\over 2}(q+r)p.$$
I hope you can see an identical argument can be used to compare the other pairings of expressions for area, and we end up with:
$${1\over 2}(q+p)r > {1\over 2}(p+r)q > {1\over 2}(r+q)p.$$
So the fences should be arranged with $r$ being the middle one in order to enclose the maximum area.
