Inequalities
-

-
 problem
problemShades of Fermat's Last Theorem
The familiar Pythagorean 3-4-5 triple gives one solution to (x-1)^n + x^n = (x+1)^n so what about other solutions for x an integer and n= 2, 3, 4 or 5?
-
 problem
problemTwo cubes
Two cubes, each with integral side lengths, have a combined volume equal to the total of the lengths of their edges. How big are the cubes? [If you find a result by 'trial and error' you'll need to prove you have found all possible solutions.] -
 problem
problemCode to zero
Find all 3 digit numbers such that by adding the first digit, the square of the second and the cube of the third you get the original number, for example 1 + 3^2 + 5^3 = 135. -
 problem
problemWithout calculus
Given that u>0 and v>0 find the smallest possible value of 1/u + 1/v given that u + v = 5 by different methods. -
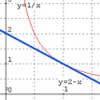 problem
problemReciprocals
Prove that the product of the sum of n positive numbers with the sum of their reciprocals is not less than n^2. -
 problem
problemDiverging
Show that for natural numbers x and y if x/y > 1 then x/y>(x+1)/(y+1}>1. Hence prove that the product for i=1 to n of [(2i)/(2i-1)] tends to infinity as n tends to infinity. -
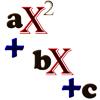 problemFavourite
problemFavouriteQuadratic harmony
Find all positive integers a and b for which the two equations: x^2-ax+b = 0 and x^2-bx+a = 0 both have positive integer solutions. -
 problemFavourite
problemFavouriteUnit interval
Take any two numbers between 0 and 1. Prove that the sum of the numbers is always less than one plus their product? -
 problem
problemClimbing
Sketch the graphs of y = sin x and y = tan x and some straight lines. Prove some inequalities.
