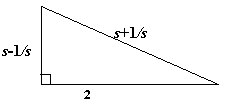This is another solution by Yatir from Maccabim-Reut High
School, Israel.
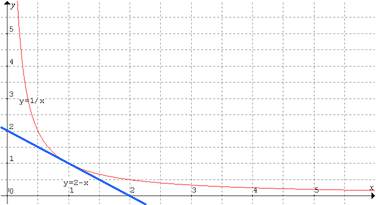
First let's prove that the sum of a positive number and its
reciprocal is at least 2. It is clearly true for all x that
$(x-1)^2 \geq 0$, hence $x^2-2x+1 \geq 0$ and it follows that $x^2
+ 1 \geq 2x$. Since $x> 0$ there is no harm in dividing by $x$
proving that for all $x> 0$
$$x + {1\over x} \geq 2.$$
Another challenge is to use the hints given by the two
illustrations in the question and to give alternative proofs that
the sum of a positive number and its reciprocal is greater than or
equal to 2.
Yatir uses this inequality when he sums k fractions and their
reciprocals in the following proof. Can you use a similar method to
give a shorter proof of the result without resorting to
mathematical induction? You will need to expand the expression
given in (1), collect pairs of terms, decide how many pairs there
are and use the inequality for each of the pairs of terms.
We have to prove that:
$$(x_1 + x_2 + \cdots + x_n)({1\over x_1}+ {1\over x_2}+
\cdots + {1\over x_n}) \geq n^2.\quad (1)$$
Let's carry on by induction, first for $n=1$ we have $x_1
\times {1\over x_1} = 1 \geq 1^2$ so this part is proved.
Let's assume that it is true for a positive integer $n=k$:
$$(x_1 + x_2 + \cdots + x_k)({1\over x_1}+ {1\over x_2}+ \cdots +
{1\over x_k}) \geq k^2.$$
Now let's prove it for $n=k+1$. We have
$$\eqalign { (x_1 + x_2 + \cdots + x_k + x_{k+1})({1\over
x_1}+ {1\over x_2}+ \cdots + {1\over x_k} + {1\over x_{k+1}})
&= (x_1 + x_2 + \cdots + x_k)({1\over x_1}+ {1\over x_2}+
\cdots + {1\over x_k})\cr &+ x_{k+1}({1\over x_1}+ {1\over
x_2}+ \cdots + {1\over x_k})\cr &+ {1\over x_{k+1}}(x_1 + x_2 +
\cdots + x_k)\cr &+ 1 \cr &\geq k^2 +
\sum_{i=1}^k({x_{k+1}\over x_i}+ {x_i\over x_{k+1}})+ 1. \cr
}$$
We have used the induction assumption that the result is true
for $n=k$ in the last line. By opening this up we see that we have
the sum of $k$ positive numbers and their reciprocals. Since each
one of them is at least 2 we replace each of them by 2 so the
inequality becomes:
$$\eqalign { (x_1 + x_2 + \cdots + x_k + x_{k+1})({1\over
x_1}+ {1\over x_2}+ \cdots + {1\over x_k} + {1\over x_{k+1}}) \geq
k^2 + 2k + 1 = (k+1)^2 \cr }$$
This proves the inequality for $n=k+1$ and so, by the axiom of
induction, the result is true for all positive
integers.