Creating and manipulating expressions and formulae

Jo made a cube from some smaller cubes, painted some of the faces of the large cube, and then took it apart again. 45 small cubes had no paint on them at all. How many small cubes did Jo use?

Can you match up these equivalent algebraic expressions?

The heptathlon is an athletics competition consisting of 7 events. Can you make sense of the scoring system in order to advise a heptathlete on the best way to reach her target?

Charlie likes tablecloths that use as many colours as possible, but insists that his tablecloths have some symmetry. Can you work out how many colours he needs for different tablecloth designs?

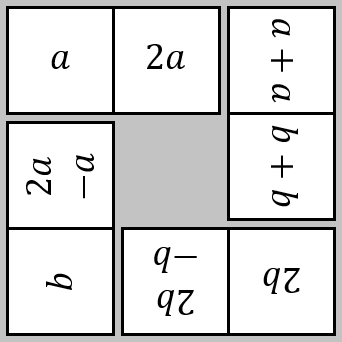
What is special about the difference between squares of numbers adjacent to multiples of three?

If you know the perimeter of a right angled triangle, what can you say about the area?

Can you explain what is going on in these puzzling number tricks?

There are unexpected discoveries to be made about square numbers...