Plum Tree
Problem
Each of the numbers $1$ to $15$ is used to label one of the vertices or one of the edges of this plum tree.
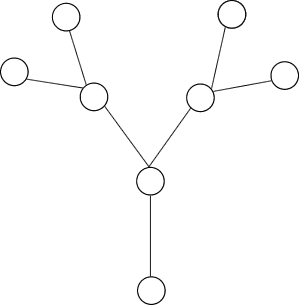
A graph is said to be 'vertex magic' if the sum of the numbers on a vertex and on all the edges joined to that vertex is the same for each vertex. We call this the 'magic sum'.
A graph is said to be 'edge magic' if, for each edge, the sum of the three numbers, on the edge and the two vertices at its ends, is the same. This is called the 'magic constant'.
A graph is said to be 'totally magic' if it is both vertex magic and edge magic. The labellings to make it vertex magic and to make it edge magic do not have to be the same and the magic sum and magic constant do not have to be the same .
Prove that this plum tree can be labelled to make it totally magic. Is there more than one edge magic labelling and more than one vertex magic labelling apart from symmetries and apart from simply exchanging the number on an extreme vertex with the number on its branch?
Can you construct a tree of your own that is totally magic?
Getting Started
This is a long and detailed hint which provides ideas, not just for this particular problem, but also for other magic graph problems where similar reasoning can be used.
Vertex Magic Investigation
There are 8 vertices and 7 edges. Let's suppose the magic constant is $h$ and this is the same at each vertex. The total of all the numbers $1 + 2 + ... + 15 = 120$ but the numbers on the edges, say $a,b,c,d,e,f,g$ are each counted twice so
$$(a+b+c+d+e+f+g)+120=8h.$$
So $a+b+c+d+e+f+g$ is a multiple of 8 and it is at least $1+2+...+7=28$ so it must be $32$ or more. Hence $8h\geq 152$ and $h\geq 19$.
It is easy to check, in a similar way, for the largest value that $h$ can take. Now it is a matter of systematically checking the possibilities for magic labellings with $h=19$ etc.
Edge Magic Investigation
How do we discover what edge magic graphs there are? Here the three order-3 vertices $a, b,c$ are counted three times and the sum of all the numbers is again $120$.
$$2(a+b+c)+120=7k.$$
Hence $k$ is even and since $a+b+c\geq 6$ we have $7k\geq 120+12=132$ and so $k\geq 20$.
If $k=20$ then $a+b+c=10$ so this triple is $1+2+7$ or $1+3+6$ or $1+4+5$ or $2+3+5$.
The possible edge sums for $k=20$ are:
$1+4+15$, $1+5+14$, $1+6+13$, $1+7+12$, $1+8+11$, $1+9+10$, $2+3+15$, $2+4+14$, $2+5+13$, $2+6+12$, $2+7+11$, $2+8+10$, $3+4+13$, $3+5+12$, $3+6+11$, $3+7+10$, $3+8+9$, $4+5+11$, $4+6+10$, $4+7+9$, $5+6+9$, $5+7+8$.
It is easy to find the edge magic labelling for $k=20$.
Moreover, substituting $16-P$ for each of the P-labels giving a magic total of $k$ will give the same numbers $1$ to $15$ and a magic total of $48-k$. So for all the magic graphs you find with a magic total of $20$ there are corresponding graphs with a magic total of $28$.
It is left for you to find the edge magic labels for $k=20$ and for $k=22$ (and correspondingly $k=26$) andfor $k=24$. Remember $k$ must be even and at least $20$ so these are the only possibilities.
Student Solutions
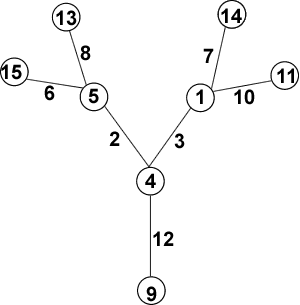
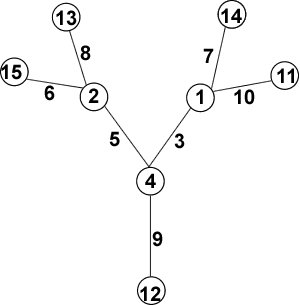
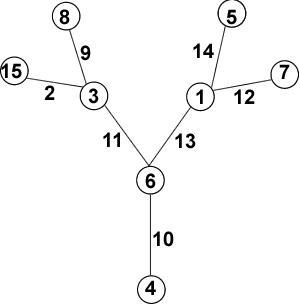
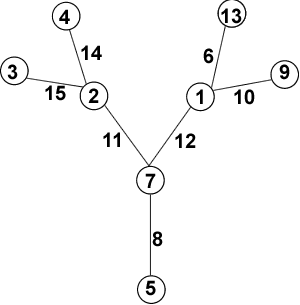
There are many possible magic labellings and it is possible to work systematically and to use simple algebraic arguments to find them all (see the hint to get started). Also it is possible to find a magic vertex labelling and a magic edge labelling for 20. Jo sent us her labelled trees:
I thought about what conditions I had, and used them to narrow down the number of possibilities, then just tried some things out, and they worked! I expect that there are lots more possibilities, but I don't know. Anyway, here are my trees.
Vertex magic (each with sum $21$):