Perception versus reality
Infographics are a powerful way of communicating statistical information. Can you come up with your own?
How old am I?
In 15 years' time my age will be the square of my age 15 years ago. Can you work out my age, and when I had other special birthdays?
Chances are
Which of these games would you play to give yourself the best possible chance of winning a prize?

Salinon
This shape comprises four semi-circles. What is the relationship between the area of the shaded region and the area of the circle on AB as diameter?
The better choice
Here are two games you can play. Which offers the better chance of winning?
Finding factors
Can you find the hidden factors which multiply together to produce each quadratic expression?
Factorising with multilink
Can you find out what is special about the dimensions of rectangles you can make with squares, sticks and units?
Odds and evens made fair
In this follow-up to the problem Odds and Evens, we invite you to analyse a probability situation in order to find the general solution for a fair game.
Difference of two squares
What is special about the difference between squares of numbers adjacent to multiples of three?
The square under the hypotenuse
Can you work out the side length of a square that just touches the hypotenuse of a right angled triangle?
Picture story
Can you see how this picture illustrates the formula for the sum of the first six cube numbers?
Triangle midpoints
You are only given the three midpoints of the sides of a triangle. How can you construct the original triangle?
Doesn't add up
In this problem we are faced with an apparently easy area problem, but it has gone horribly wrong! What happened?
Two ladders
Two ladders are propped up against facing walls. At what height do the ladders cross?
CD Heaven
All CD Heaven stores were given the same number of a popular CD to sell for £24. In their two week sale each store reduces the price of the CD by 25% ... How many CDs did the store sell at each price?
In a box
Chris and Jo put two red and four blue ribbons in a box. They each pick a ribbon from the box without looking. Jo wins if the two ribbons are the same colour. Is the game fair?
Semi-detached
A square of area 40 square cms is inscribed in a semicircle. Find the area of the square that could be inscribed in a circle of the same radius.

Triangles and petals
An equilateral triangle rotates around regular polygons and produces an outline like a flower. What are the perimeters of the different flowers?
The spider and the fly
A spider is sitting in the middle of one of the smallest walls in a room and a fly is resting beside the window. What is the shortest distance the spider would have to crawl to catch the fly?
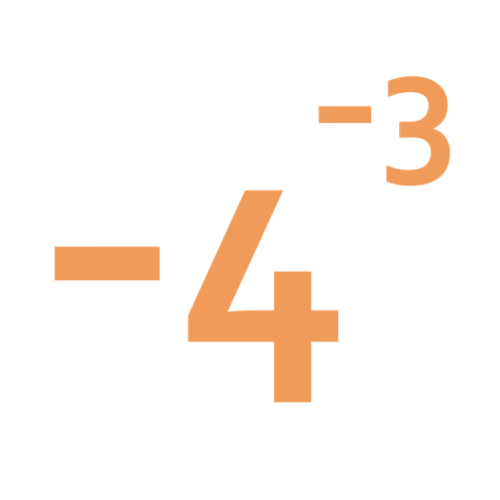
Negative powers
What does this number mean? Which order of 1, 2, 3 and 4 makes the highest value? Which makes the lowest?
LCM Sudoku
Here is a Sudoku with a difference! Use information about lowest common multiples to help you solve it.

Immersion
Various solids are lowered into a beaker of water. How does the water level rise in each case?
Partly painted cube
Jo made a cube from some smaller cubes, painted some of the faces of the large cube, and then took it apart again. 45 small cubes had no paint on them at all. How many small cubes did Jo use?
Multiplication arithmagons
Can you find the values at the vertices when you know the values on the edges of these multiplication arithmagons?
Which list is which?
Six samples were taken from two distributions but they got muddled up. Can you work out which list is which?
Kite in a square
Can you make sense of the three methods to work out what fraction of the total area is shaded?
Napkin
A napkin is folded so that a corner coincides with the midpoint of an opposite edge. Investigate the three triangles formed.
Far horizon
An observer is on top of a lighthouse. How far from the foot of the lighthouse is the horizon that the observer can see?
Areas and ratios
Do you have enough information to work out the area of the shaded quadrilateral?
