Factorising with multilink
Problem
For this problem, you will either need multilink cubes or these sets of number base sheets to cut out: Base Three Base FourBase Five Base Six.
In the video below, Charlie and Becky show how you can make rectangles using sets of squares, sticks and units.
Can you make a rectangle to represent $x^2 + 7x + 12$?
Can you do it in more than one base?
Watch the video below to see how Charlie and Becky tackled this question:
Take 1 square and 12 units in your chosen base. Put them together with some sticks to make rectangles that will work in all bases.
Charlie and Becky made $x^2 + 7x + 12$ into a rectangle with length $x+4$ and width $x+3$.
How many different rectangles can you make?
What do you notice about the dimensions of your rectangles?
Imagine you had 1 square, lots of sticks and 100 units. What can you say about the dimensions of the rectangles it is possible to make?
Now, take 1 square and 12 sticks in your chosen base. Put them together with some units to make rectangles that will work in all bases.
How many different rectangles can you make?
What do you notice about the dimensions of your rectangles?
Imagine you had 1 square, 100 sticks and lots of units. What can you say about the dimensions of the rectangles it is possible to make?
If you had 1 square, $p$ sticks and $q$ units, what can you say about the dimensions of the rectangles it is possible to make?
Extension
Think about the rectangles it's possible to make if you use two, three, four... squares, some sticks and some units.
You may also be interested in the other problems in our Getting started, getting stuck Feature.
Many thanks to Kenneth Ruthven and Paul Andrews whose ideas inspired this problem.
Getting Started
Start with families of examples such as:
$x^2 + 3x + 2$
$x^2 + 4x + 3$
$x^2 + 5x + 4$
...
What do you notice?
Can you explain why?
Student Solutions
Luke from London Oratory School explained how the situation can be shown using algebra:
The red section (made of sticks) consists of two rectangles with dimensions $a, x$ and $b, x$. Therefore the red area is equal to $ax+bx$, which equals $x(a+b)$.
We can see that the area of the blue section will always have dimensions $a$ and $b$, so its area is equal to $ab$, if it Ê»ï¬llsʼ the gap created by the red area.
The total area is equal to the sum of these component areas.
Thus you can make a rectangle for all bases for expression of the form $x^2 + x(a+b) + ab$ where $a$ and $b$ are positive integers. The rectangle has dimensions $(x+a)$ by $(x+b)$.
1 square, lots of sticks and 12 or 100 units
Mahdi, Hamaad and Khalid used algebra again. Here is Mahdi's work for 12 sticks:
This is Hamaad and Khalid's work for 100 sticks:
1 square, 12 or 100 sticks and lots of units
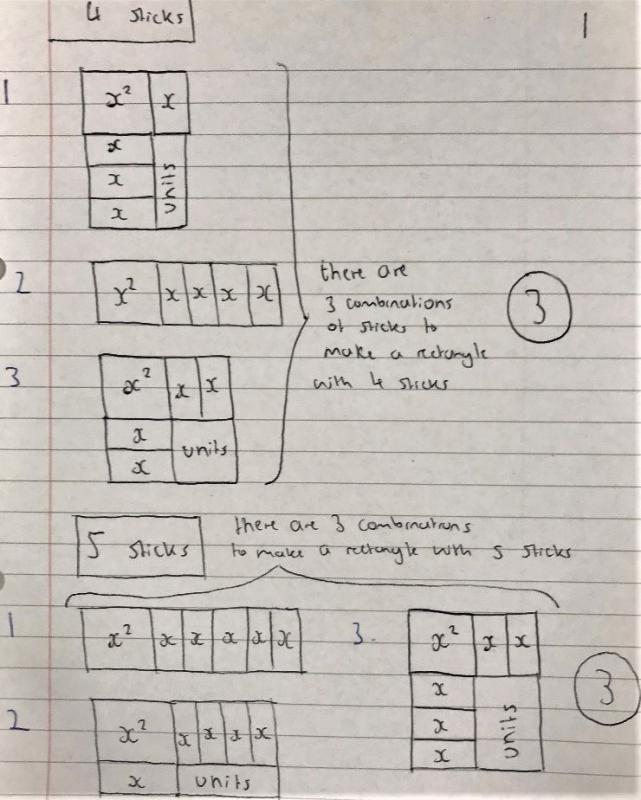
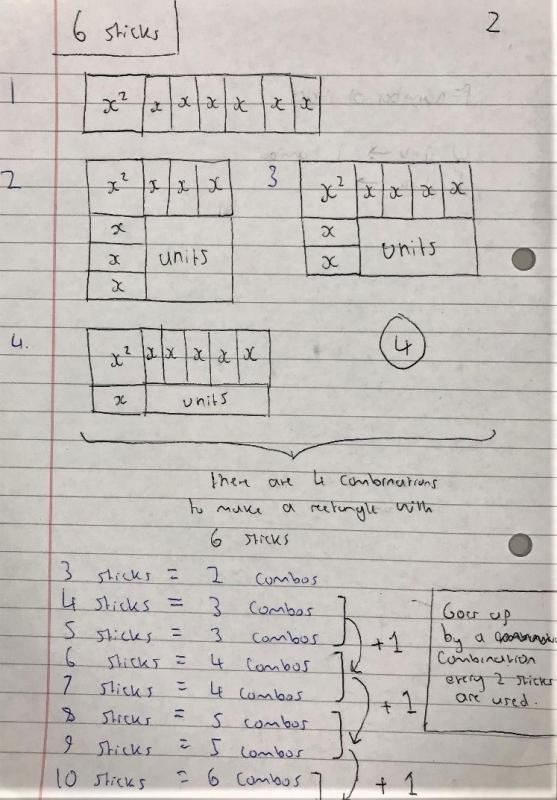
Hadi from Michaela Community School in the UK started with smaller numbers of sticks and then spotted a pattern:
Mahdi from Mahatma Gandhi International School in India used algebra:
Hamaad and Khalid from Michaela Community School and Mahdi used the same approah for 100 sticks. This is Hamaad and Khalid's work:
For $p$ sticks and $q$ units
Mahdi approached this algebraically:
So how many different rectangles can you make with $p$ sticks and $q$ units?
Teachers' Resources
Why do this problem?
When students first meet factorisation, they often don't make the connection between factorising an algebraic expression and breaking a number into factor pairs. This problem introduces factorisation using a visual representation that allows students to make that connection and discover for themselves the properties necessary for a quadratic expression to factorise.
This problem is a nice example of a Low Threshold High Ceiling task, as students can use the representation to factorise more and more complicated examples. You can read more about Low Threshold High Ceiling tasks in this article.
Possible approach
Take a look at the second video to see how Becky and Charlie resolve their different rectangles into one that works for both of them.
Key question
What is the connection between the number of sticks you need, the number of units you need, and the dimensions of the rectangle?
Possible support
Start students off on families of examples such as:
$x^2 + 3x + 2$
$x^2 + 4x + 3$
$x^2 + 5x + 4$
...
Possible extension
Think about the rectangles it's possible to make if you use 2, 3, 4... squares, some sticks and some units.
Finding Factors consolidates the ideas met here and has factorisations which require negative terms.