Three cubes
1. The distance between centres of two adjacent faces of a cube is $8$cm.
What is the side length of the cube?
2. I can make an equilateral triangle by cutting off the corner of a cube.
If the area of the largest equilateral triangle I can create in this way is $140$cm$^2$, what is the side length of this cube?
3. A third cube has an edge length of $12$cm.
At each vertex, a tetrahedron with three mutually perpendicular edges of length $4$cm is cut away.
Can you find the volume and the surface area of the remaining solid?
Thank you Andrew Clark for this solution.
1. The distances between the centres of two adjacent faces of another cube is $8$cms. What is the side length of this cube?
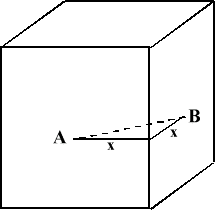
Let the side length of the cube be $ 2x $. From the centre points A and B of both faces to the line at which their planes meet is $ x $, and AB ($ = 8 $) is the hypotenuse of a right angled triangle whose other two sides have length $ x $ . Therefore $ 2x^2 = 8^2 $ , so that $ x= \sqrt{32} $ , and the length of the side is $ 8\sqrt{2} $ .
2. It is known that the area of the largest equilateral triangular section of a cube is $140$cm$^2$ . What is the side length of the cube?
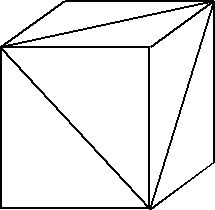
Cube with equilateral triangle section.
Let the sides of the equilateral triangle have length $ a $; then the area of the triangle is $ (a/2)(a\sqrt{3}/2) = a^2\sqrt{3}/4 $. As the area of the triangle is $ 140 {\rm cm}^2 $, $ a^2 = 560/\sqrt{3} $. The length of the diagonal of a face of the cube is $ a $; let $ b $ be the length of a side of the cube. Then, by Pythagoras' Theorem, $ 2b^2 = 560/\sqrt{3} $ so that $ b=12.7 $ to three
significant figures.
3. Another cube has an edge length of $12$cms. At each vertex a tetrahedron with three mutually perpendicular edges of length $4$cms is sliced away. What is the surface area and volume of the remaining solid?
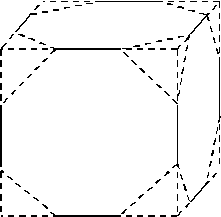
From each face of the cube we remove four triangles whose total area is $ 32 {\rm cm}^2 $ . Thus the area left is $ 144-32 = 112 {\rm cm}^2 $ . There are six such faces giving an area of $ 672 {\rm cm}^2 $ . \par In addition, there are eight equilateral triangular faces of side length $ 4\sqrt{2} $ . The total area of these is $ 8 \times 8\sqrt{3} = 64\sqrt{3} {\rm cm}^2 $ . Thus the total surface area is $ 672 + 64\sqrt{3} = 783 {\rm cm}^2 $ to the nearest square centimetre.
The volume of a tetrahedron is $ (1/3) \times \hbox{(area of base)} \times \hbox{height} $ . Consider one of the tetrahedra, and take one of the right-angled triangles as its base; then its volume is $ (1/3) \times 8 \times 4 = 32/3 $ . Thus the volume of the remaining solid is $ 12^3 - (8\times 32)/3 = 1643 {\rm cm}^3 $ to the nearest cubic centimetre.
Why do this problem?
This problem presents a series of three-dimensional challenges which encourage the learner to visualise a solid and then use two-dimensional representations to help them to reach a solution. On the way to a solution, there are opportunities to practise using trigonometry and Pythagoras, as well as formulas for volume.
Possible approach
Each part of this problem could be tackled by small groups who could then present their solution to other groups. This gives students time to share their ideas and practise their arguments before presenting to another group, who should act as critical friends. Make it clear that all members of the group are expected to participate in the presentation. For each problem, it is best to take some time to visualise what is being asked, and then draw some diagrams to see what calculations will be necessary.
The third problem is about volume and surface area. In order to work these out, learners will have to calculate the dimensions of a tetrahedron cut from the corner of a cube.
Key questions
What two-dimensional diagrams can be drawn to help to solve the problems?
Possible support
Learners who have not met or are not confident with trigonometry and Pythagoras could solve parts of the problem using scale drawing.
Possible extension
The Spider and the Fly gives another opportunity to visualise a problem in three dimensions.