Working systematically
-

-
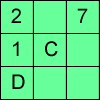 problem
problemAlphabetti Sudoku
This Sudoku requires you to do some working backwards before working forwards.
-
 problem
problemMini Kakuro
The sum of each column and row in this grid give the totals as shown. What number goes in the starred square?
-
 problem
problemDicey directions
An ordinary die is placed on a horizontal table with the '1' face facing East... In which direction is the '1' face facing after this sequence of moves? -
 problem
problemSimple train journeys
How many different journeys could you make if you were going to visit four stations in this network? How about if there were five stations? Can you predict the number of journeys for seven stations? -
 problem
problem9 weights
You have been given nine weights, one of which is slightly heavier than the rest. Can you work out which weight is heavier in just two weighings of the balance? -
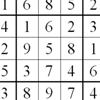 problem
problemTwin chute-swapping Sudoku
A pair of Sudokus with lots in common. In fact they are the same problem but rearranged. Can you find how they relate to solve them both?
-
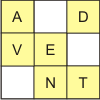 problem
problemAdvent Sudoku
Rather than using the numbers 1-9, this sudoku uses the nine different letters used to make the words "Advent Calendar".
-

-
 problem
problemSimultaneous equations Sudoku
Solve the equations to identify the clue numbers in this Sudoku problem.
