Cryptarithms
Can you crack these cryptarithms?
Problem
Cryptarithms printable worksheet
A cryptarithm is a mathematical puzzle where the digits in a sum have been replaced by letters.
In each of the puzzles below, each letter stands for a different digit.
Bearing in mind that none of the numbers below have 0 as a leading digit, can you find a solution to all of these cryptharithms?
Do any of them have more than one solution?
| 1. | Image
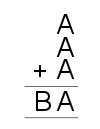
| 2. | Image

| 3. | Image

| 4. | Image

|
| 5. | Image
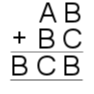
| 6. | Image
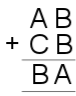
| 7. | Image

| 8. | Image
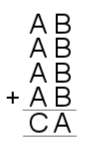
|
| 9. | Image
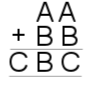
| 10. | Image
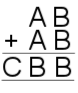
| 11. | Image
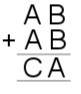
| 12. | Image
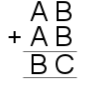
|
| 13. | Image
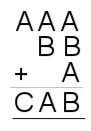
| 14. | Image
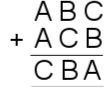
| 15. | Image
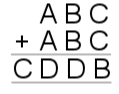
| 16. | Image
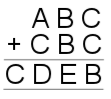
|
| 17. | Image
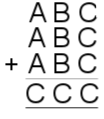
| 18. | Image
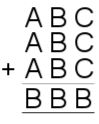
| 19. | Image
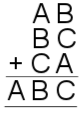
| 20. | Image
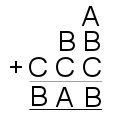
|
| 21. | Image
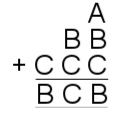
| 22. | Image

| 23. | Image
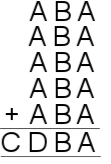
|
Final Challenge
Is it possible for all of the digits 1 to 9 to appear exactly once in the addition below?
+ # # #
# # #
Using each digit from 1 to 9 once, what is the largest sum you can obtain in the addition above?
If you enjoyed this problem, you may also like to take a look at Two and Two.
With thanks to Don Steward, whose ideas formed the basis of this problem.
Getting Started
Try to think about the biggest or smallest numbers you could add together in each case.
Does that tell you anything about the digits of the number that they sum to ?
If you add two $2$ digit numbers together to make a $3$ digit number, what could the first digit of the answer be?
Student Solutions
We had lots of great solutions submitted for this problem - thank you to everybody who sent in a solution!
Here is a list of all the solutions we have managed to find for each puzzle. Please let us know if you discover any more!
1) $A=5, B=1$.
2) $A=1, B=9, C=0$.
3) $A=9, B=1, C=0$.
4) $A=9, B=2, C=1, D=0$.
5) $A=9, B=1, C=0$.
6) $A=2, B=6, C=3$
or $A=4, B=7, C=2$
or $A=6, B=8, C=1$.
7) $A=2, B=1, C=9$.
8) $A=2, B=3, C=9$.
9) $A=9, B=2, C=1$.
10) $A=5, B=0, C=1$.
11) $A=2, B=1, C=4$
or $A=2, B=6, C=5$
or $A=4, B=2, C=8$
or $A=4, B=7, C=9$.
12) $A=1, B=2, C=4$
or $A=2, B=4, C=8$
or $A=2, B=5, C=0$
or $A=3, B=7, C=4$
or $A=4, B=9, C=8$.
13) $A=5, B=9, C=6$.
14) $A=4, B=5, C=9$.
15) $A=7, B=2, C=1$.
16) $A=9, B=2, C=1, D=0, E=4$.
17) $A=1, B=8, C=5$.
18) $A=1, B=4, C=8$.
19) $A=1, B=9, C=8$.
20) $A=4, B=7, C=6$.
21) $A=2, B=9, C=8$.
22) $A=9, B=4, C=1, D=6$.
23) $A=5, B=7, 2, D=8$.
Well done to everyone who got any of these right!
Some of you gave really good explanations for how you worked out your answers.
Charlotte from St. Stephen's School in Australia explained how she got the answer to the first problem:
$A+A+A= BA$. $A+A+A$ must equal a number above $10$ because it equals a
two digit number ($BA$). Then you must work out which three numbers under $10$
are added together to equal a number under $30$ with the same second digit. $A$
also has to be $4$ or above because $3\times3=9$ which is not a two digit number.
Then try trial and error with this information
$4+4+4= 12$
$5+5+5= 15$
$6+6+6= 18$
$7+7+7= 21$
$8+8+8= 24$
$9+9+9= 27$
By doing this you will be able to find out your answer.
$A= 5$
$B= 1$
Several people worked out that for the next few problems, the first digit of the total would be $1$. MJ from the Bourne Academy explained it like this:
I just kept thinking about how many digits were being added and found each time there was a key letter I could work out each time - $e.g.$ on question $7$, $B$ had to be $1$ as you cannot add two $2$-digit numbers together and get a number above $198$.
Lots of people used trial and error for the later problems, but some found patterns in the numbers. Here is Monique's (from St. Stephen's School) answer to question $12$:
$B$ is equal to half of $C$ and $A$ is equal to half of $B$. $A$ has to be smaller than $5$ otherwise the sum would be a $3$-digit number. $B$ can only be equal to $2$ or $4$ because they are the only numbers that can be equally divided into $A$ in the tens column.
Zach used colours to help visualise how the problems worked:
To solve the puzzles, I looked at how the letters were arranged and just thought about how numbers work.
I found that if I used colour blocks instead of letters, I could more easily visualise the relationships and very quickly arrive at the answer. Sometimes I used algebra, but generally I just looked for patterns. The questions also built understanding, and logic established in earlier questions could be assumed later on.
Here is how he used colours to help him with question $20$:

"There is a number bond of $10$ in the units column, so $A+C=10$, as $B+10$ is the only feasible sum in the units column that will gie $B$ as a unit. I used trial and error to investigate number bonds of $10$, pairing $A=1$ with $C=9$ etc... $B$ then became the balancing figure. The only combination that worked was $A=4$, $B=7$, $C=6$.
Thank you again to everyone who submitted a solution!
Teachers' Resources
This printable worksheet may be useful: Cryptarithms.
Why do this problem?
This problem builds on students’ fluency in adding integers and encourages them to choose possible integers based on their properties. Students will practice mathematical reasoning and systematic working.
Possible approach
Introduce questions in batches, starting with just questions 1-4 or even just 1 and 2. Ask students to work in pairs or groups to find answers, potentially stopping to give hints of which letter to focus on to begin each question.
Once students have attempted these questions, discuss their methods. Which number facts did they use? How did they know there weren't more answers? You might want to take notes on the board for students to refer back to later.
More questions can now be introduced in batches. Several of the questions - e.g 6 & 7, 11 & 12, 15 & 16, 17 & 18, 20 & 21 - pair together nicely and could be focused on together, if needed. There is opportunity to split these pairs amongst the class, which would allow for comparison between the differences in very similar questions.
Alternatively, all of the questions – perhaps without the extension – could be shown at once, with students allowed to choose which questions they attempt, either on their own or in pairs/groups.
Towards the end, the final challenge can then be offered. This can be attempted by all of the students, regardless of how far they have got with the other questions (although you might want to save it for later if the students have made little progress). You could pose the final challenge to the whole group, and allow students to share their best possible answer. Give students time to try to match and beat the best answers before asking those with the highest totals to share their methods.
Key questions
How can we prove we have found all of the solutions?
What number facts can we use?
Possible support
Replace one letter with its correct number in the questions. Begin by considering numerical facts, then introduce reasoning and systematic working.
Possible extension
Students could invent their own cryptarithms. How many solutions will their cryptarithm have? Can they create one with one, two, three, no solutions?
Two and Two continues the use of cryptarithms and extends ideas of mathematical reasoning.
