Reasoning, convincing and proving

problem
In constantly passing

Age

14 to 16

Challenge level

A car is travelling along a dual carriageway at constant speed. Every 3 minutes a bus passes going in the opposite direction, while every 6 minutes a bus passes the car travelling in the same direction. Buses leave the depot at regular intervals; they travel along the dual carriageway and back to the depot at a constant speed. At what interval do the buses leave the depot?
problem
Tetra perp

Age

16 to 18

Challenge level

Show that the edges $AD$ and $BC$ of a tetrahedron $ABCD$ are mutually perpendicular if and only if $AB^2 +CD^2 = AC^2+BD^2$. This problem uses the scalar product of two vectors.
problem
Three by one

Age

16 to 18

Challenge level

There are many different methods to solve this geometrical problem - how many can you find?
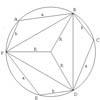
problem
Hexy-metry

Age

14 to 16

Challenge level

A hexagon, with sides alternately a and b units in length, is inscribed in a circle. How big is the radius of the circle?
problem
Ordered sums

Age

14 to 16

Challenge level

Let a(n) be the number of ways of expressing the integer n as an ordered sum of 1's and 2's. Let b(n) be the number of ways of expressing n as an ordered sum of integers greater than 1. (i) Calculate a(n) and b(n) for n<8. What do you notice about these sequences? (ii) Find a relation between a(p) and b(q). (iii) Prove your conjectures.
problem
Pythagoras for a tetrahedron

Age

16 to 18

Challenge level

In a right-angled tetrahedron prove that the sum of the squares of the areas of the 3 faces in mutually perpendicular planes equals the square of the area of the sloping face. A generalisation of Pythagoras' Theorem.
problem
Rational round

Age

16 to 18

Challenge level

Show that there are infinitely many rational points on the unit circle and no rational points on the circle x^2+y^2=3.
problem
Leonardo's problem

Age

14 to 18

Challenge level

A, B & C own a half, a third and a sixth of a coin collection. Each grab some coins, return some, then share equally what they had put back, finishing with their own share. How rich are they?
problem
Sixty-seven squared

Age

16 to 18

Challenge level

Evaluate these powers of 67. What do you notice? Can you convince someone what the answer would be to (a million sixes followed by a 7) squared?
problem
Eyes down

Age

16 to 18

Challenge level

The symbol [ ] means 'the integer part of'. Can the numbers [2x]; 2[x]; [x + 1/2] + [x - 1/2] ever be equal? Can they ever take three different values?