Zig Zag
Problem
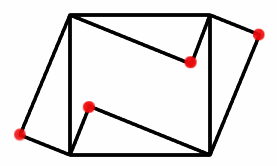
Four identical right angled triangles are drawn on the sides of a square. Two face out, two face in. Why do the four vertices marked with dots lie on one line?
Student Solutions
Four identical right angled triangles are drawn on the sides of a square. Two face out, two face in. Congratulations Soh Yong Sheng of Raffles Institution, Singapore and James of Hethersett High School for your solution. The image

can be further expanded into a diagram containing 3 squares of which two are the same size.
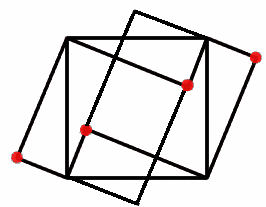
The two smallest quadrilaterals produced are squares as their sides are all of the same length equal to the shortest side of the triangle. The dots will form one line containing the diagonals of the three squares as the sides of the squares are all perpendicular or parallel to each other.
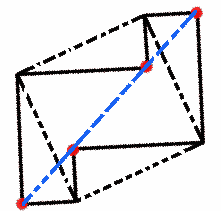
Here is another way of looking at it.
Teachers' Resources
Why do this problem :
There is an important configuration of four congruent right-angled triangles which make a square in two ways. Either the sides of the square are formed from each triangle's hypotenuse, or from putting together the two lengths adjacent to the right angle in the triangle. This problem uses two of the four matching points from each configuration. The other two points are not shown and so exploring this problem will draw students into discovering this arrangement and also provides experience in how a situation may sometimes present as only part of a more meaningful or useful 'whole'.
Possible approach :
Ask students to guess whether the four points indicated do or do not lie on a straight line, especially once the triangles are free to move as a general right-angled triangle.
There is scope for an activity to draw accurately the configuration shown in the problem, but with right-angled triangles which students form for themselves.
Alternatively use a Dynamic Geometry package, but in either case move the group into a discussion about whether these four points form one straight line or not.
The aim, as the exploration continues, is to cause some high-energy discussion shot-through with geometric reasoning, where students challenge each other to say why they are sure that this is one line. And as they do that the configuration illustrated above is discovered along the way.
Key questions :
-
What does this diagram show ?
-
Are the four points aligned or just close to it, and would that answer change if the arrangement used right-angled triangles of another proportion ?
-
How can you be sure of that ?
-
What perspective would you try to share with others to help them see and enjoy the relationships within this arrangement ?
