Reasoning, convincing and proving

problem
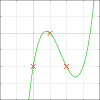Interpolating polynomials

Age

16 to 18

Challenge level

Given a set of points (x,y) with distinct x values, find a polynomial that goes through all of them, then prove some results about the existence and uniqueness of these polynomials.
problem
Olympic measures

Age

11 to 14

Challenge level

These Olympic quantities have been jumbled up! Can you put them back together again?
problem
The fastest cyclist

Age

14 to 16

Challenge level

Andy is desperate to reach John o'Groats first. Can you devise a winning race plan?
problem
Olympic triathlon

Age

14 to 16

Challenge level

Is it the fastest swimmer, the fastest runner or the fastest cyclist who wins the Olympic Triathlon?
problem
Nutrition and cycling

Age

14 to 16

Challenge level

Andy wants to cycle from Land's End to John o'Groats. Will he be able to eat enough to keep him going?
problem
Factorising with multilink

Age

14 to 16

Challenge level

Can you find out what is special about the dimensions of rectangles you can make with squares, sticks and units?
problem
Always a multiple?

Age

11 to 14

Challenge level

Think of a two digit number, reverse the digits, and add the numbers together. Something special happens...
problem
Double trouble

Age

14 to 16

Challenge level

Simple additions can lead to intriguing results...
problem
Round a hexagon

Age

7 to 11

Challenge level

This problem shows that the external angles of an irregular hexagon add to a circle.
problem
Walking round a triangle

Age

5 to 7

Challenge level

This ladybird is taking a walk round a triangle. Can you see how much she has turned when she gets back to where she started?