Modular arithmetic

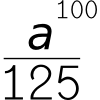problem

Remainder Hunt

Age

16 to 18

Challenge level

What are the possible remainders when the 100-th power of an integer is divided by 125?
problem

Double Time

Age

16 to 18

Challenge level

Crack this code which depends on taking pairs of letters and using two simultaneous relations and modulus arithmetic to encode the message.
problem
Favourite

Odd Stones

Age

14 to 16

Challenge level

On a "move" a stone is removed from two of the circles and placed in the third circle. Here are five of the ways that 27 stones could be distributed.
problem

A One in Seven Chance

Age

11 to 14

Challenge level

What is the remainder when 2^{164}is divided by 7?
problem

Modular Fractions

Age

16 to 18

Challenge level

We only need 7 numbers for modulus (or clock) arithmetic mod 7 including working with fractions. Explore how to divide numbers and write fractions in modulus arithemtic.
problem

The Public Key

Age

16 to 18

Challenge level

Find 180 to the power 59 (mod 391) to crack the code. To find the secret number with a calculator we work with small numbers like 59 and 391 but very big numbers are used in the real world for this.
problem

It Must Be 2000

Age

7 to 11

Challenge level

Here are many ideas for you to investigate - all linked with the number 2000.
problem
Favourite

Days and Dates

Age

11 to 14

Challenge level

Investigate how you can work out what day of the week your birthday will be on next year, and the year after...
problem
Favourite

Round and Round and Round

Age

11 to 14

Challenge level

Where will the point stop after it has turned through 30 000 degrees? I took out my calculator and typed 30 000 ÷ 360. How did this help?
problem
Favourite

Elevenses

Age

11 to 14

Challenge level

How many pairs of numbers can you find that add up to a multiple of 11? Do you notice anything interesting about your results?