Graph sketching
-

-
 problem
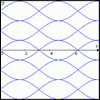
problemSine problem
In this 'mesh' of sine graphs, one of the graphs is the graph of the sine function. Find the equations of the other graphs to reproduce the pattern. -
 problem
problemMaltese cross
Sketch the graph of $xy(x^2 - y^2) = x^2 + y^2$ consisting of four curves and a single point at the origin. Convert to polar form. Describe the symmetries of the graph. -
 problem
problemMore parabolic patterns
The illustration shows the graphs of twelve functions. Three of them have equations y=x^2, x=y^2 and x=-y^2+2. Find the equations of all the other graphs. -
 problemFavourite
problemFavouriteSlide
This function involves absolute values. To find the slope on the slide use different equations to define the function in different parts of its domain. -

-
 problem
problemReaction types
Explore the rates of growth of the sorts of simple polynomials often used in mathematical modelling. -
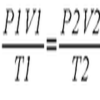 problem
problemIdeal axes
Explore how can changing the axes for a plot of an equation can lead to different shaped graphs emerging -
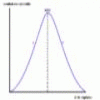 problem
problemGraphic biology
Several graphs of the sort occurring commonly in biology are given. How many processes can you map to each graph? -
 problem
problemBird-brained
How many eggs should a bird lay to maximise the number of chicks that will hatch? An introduction to optimisation.
