Guessing the graph
Can you suggest a curve to fit some experimental data? Can you work out where the data might have come from?
Age
14 to 16
Challenge level
Problem
When analysing scientific data, we often need to suggest a curve to fit a set of points, and deduce the equation of the curve.
In this set of cards, there are three data sets. Print and cut out one of the sets, shuffle the cards, and then choose a few points.
By plotting the points you are given, can you sketch a curve representing the relationship between the two variables?
The data were recorded in three sets, A, B and C, beginning at three interesting points in the experiment, so you may wish to investigate each set separately. Alternatively, you can choose to investigate the combined datasets.
Can you come up with a possible relationship using only a few pieces of data?
Start with a few data points. Plot them on a set of axes and try to fit a curve to the data.
Select some more values - do they fit your curve? Draw a new curve in a different colour if you want to change your original "best fit".
Once you are satisfied that your curve represents the data well, try working out an approximate equation for your curve, perhaps using a spreadsheet.
What sort of experiment do you think generated the data?
What sort of scientific questions might be answered by using the graph?
Based on your idea of what the experiment was, why do you think the maximum points of curves B and C are lower than the maximum point of curve A?
Getting Started
Can you find a quadratic curve that roughly fits Data Set A?
Where do you think the maximum point of the curve would be?
Consider how to turn the graph of $y=x^2$ upside down, move it up the axis, and 'squash' it to match the data.
This spreadsheet might be useful for trying out equations and seeing how closely they match the real data.
Student Solutions
Preveina from Crest Girls' Academy sent us some thoughts:
I managed to fit a curve to the data. However when I tried generating new values it didn't fit within my curve so I had to draw another curve which fitted most of the points.
By using this graph you could answer scientific questions like:
Are there any anomalous results being produced?
What relationship can be described between the variables using the graph?
When does the graph reach its peak?
Herschel, from the European School of Varese sent us a well thought out solution:
When the complete set of data is plotted on a graph, it appears as three inverted parabolas, each in the general form $y = -ax^2+bx+c$. It suggests an object such as a bouncing ball, with the data showing its displacement or height.
The ball clearly bounces twice - once at about 0.65 seconds and again at around 1.25 seconds - and it loses height each time, due to the loss of kinetic energy at the point of impact. The drastic loss of energy with each successive bounce suggests that the surface is soft (such as carpet or grass) and that the ball is a (slightly deflated) football rather than a bouncy ball.
The ball or object starts from a height of 206 at the start, and it then reaches 47 after the first bounce and 15 after the third. If we assume these values to be in centimeters, we can work out the speed of impact on each of the third bounces with the formula $v=\sqrt{2gh}$, without accounting for air resistance. We see that the velocity upon the first impact is $6.35ms^-1$, $3.04ms^-1$ upon impact for the second time and $1.71ms^-1$ the third time - in other words, it loses half its speed each time it bounces.
We can also guess that it will reach a height of around 4cm after the 3rd bounce and around 1cm after the fourth, since the maximum height each time is approximately $\frac{1}{4}$ of the previous time - 75% of the ball's energy is lost in the form of sound and heat every time it bounces.
Image
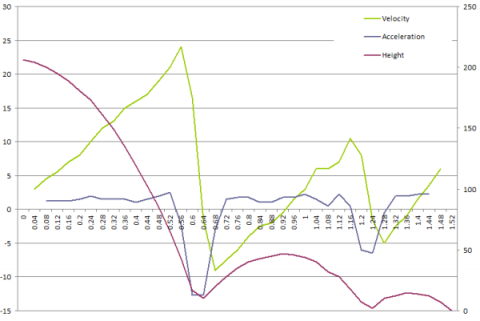
The graph plots height against time (i.e. the given data). There is also derived data, namely (downwards) velocity and acceleration. The original data (height) is on the right vertical axis while the derived data (velocity and acceleration) is on the left vertical axis, due to the difference in magnitudes of the values. Looking at the basic data, we see that the height curve is quite smooth, and the derived data shows that there is in fact a constant acceleration throughout the experiment, with the exception of the two points where the ball hits the ground and bounces. This is expected if it is a bouncing ball - it is under the constant force of gravity throughout the experiment.
A lovely analysis, Herschel - it was in fact a small plastic cube being dropped onto the carpet!
Teachers' Resources
Why do this problem?
This problem offers learners the experience of dealing with experimental data in a scientific way, challenging them to fit a curve to some real data and deduce its equation. The task offers a real-life context for manipulating quadratic graphs and considering transformations of graphs.
As the data come from an actual experiment, there is the opportunity to make links with science lessons by suggesting learners reproduce similar experiments themselves. There is the chance for genuine cross-curricular collaboration with science teachers by offering to carry out similar tasks on data collected in the course of their science lessons.
Possible approach
Introduce the learners to the idea that they will be given some data from a real scientific experiment, and their task will be to hypothesise about the relationship between the two variables using as few datapoints as possible.The activity works well in pairs, so learners can discuss their ideas as they work. They will need graph paper and to draw a horizontal axis for time going from 0 to 1.6 seconds, and a vertical axis going up to 210cm.
Explain that the problem is intended to simulate the process of scientific enquiry, where scientists have to start explaining patterns from a limited amount of data and then use further experiments to confirm or reject their hypotheses. Learners can access Data Set A by shuffling and then selecting at random cards from set A.
Once they have plotted a few points, they should sketch the line or curve they think best represents the data, and then try a few extra points to refine their conjecture if necessary. Learners could use different colours to represent the points they plotted and the lines or curves they drew at each stage.
Once they have drawn a curve that seems to match the data well, challenge them to work out a possible equation for it. The data is available in this Excel spreadsheet which learners could use to try out ideas and plot graphs matching the data closely. Alternatively, the class could discuss how a familiar curve such as $y=x^2$ could be transformed to resemble the curve they have sketched, leading on to work on transforming graphs by reflecting and stretching.
Data sets B and C can be used in the same way.
Take some time to discuss what the experiment could have been. The problem How Do You React? explores vertical motion under gravity, and could be attempted alongside this problem to explain the parabola shapes generated. Discussion of conservation of energy and elastic collisions may be appropriate with learners who have met these ideas in science lessons.
You may wish to recreate the experiment with your class - the data were gathered by filming the experiment and then advancing the video one frame at a time to take measurements. Of course, there are many other simple experiments into motion that could be carried out, with opportunities to predict the sorts of graphs that would result.
Key questions
Are the points you have best suited to a straight line or a curve?
How can we transform the graph $y=x^2$ into an inverted quadratic graph?
How can we make a quadratic graph more or less curvy?
How can we move a quadratic graph up and down the y axis?
What experiment might have been done to get these results?
Why do Data Sets B and C give a shallower curve?
Possible extension
As the experimental data represent motion of a falling object, learners could use ideas from mechanics/physics to model the situation theoretically and compare the experimental data with a theoretical value for acceleration due to gravity.
The stage 5 problem Equation Matcher offers the opportunity to consider more complicated functions passing through sets of points.