Exploring and noticing

problem

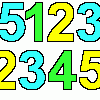1, 2, 3, 4, 5

Age

7 to 11

Challenge level

Using the numbers 1, 2, 3, 4 and 5 once and only once, and the operations x and ÷ once and only once, what is the smallest whole number you can make?
problem

Magic triangle

Age

7 to 11

Challenge level

Place the digits 1 to 9 into the circles so that each side of the triangle adds to the same total.
problem

The Pied Piper of Hamelin

Age

7 to 11

Challenge level

This problem is based on the story of the Pied Piper of Hamelin. Investigate the different numbers of people and rats there could have been if you know how many legs there are altogether!
problem

Beads

Age

7 to 11

Challenge level

Three beads are threaded on a circular wire and are coloured either red or blue. Can you find all four different combinations?
problem
Favourite

Sponge sections

Age

7 to 11

Challenge level

You have been given three shapes made out of sponge: a sphere, a cylinder and a cone. Your challenge is to find out how to cut them to make different shapes for printing.
problem
Favourite

Cut nets

Age

7 to 11

Challenge level

Each of the nets of nine solid shapes has been cut into two pieces. Can you see which pieces go together?
problem

A numbered route

Age

7 to 11

Challenge level

Can you draw a continuous line through 16 numbers on this grid so that the total of the numbers you pass through is as high as possible?
problem
Favourite

Two clocks

Age

7 to 11

Challenge level

These clocks have only one hand, but can you work out what time they are showing from the information?
problem
Favourite

Multiples grid

Age

7 to 11

Challenge level

What do the numbers shaded in blue on this hundred square have in common? What do you notice about the pink numbers? How about the shaded numbers in the other squares?
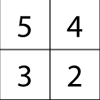
problem

Magic matrix

Age

7 to 11

Challenge level

Find out why these matrices are magic. Can you work out how they were made? Can you make your own Magic Matrix?