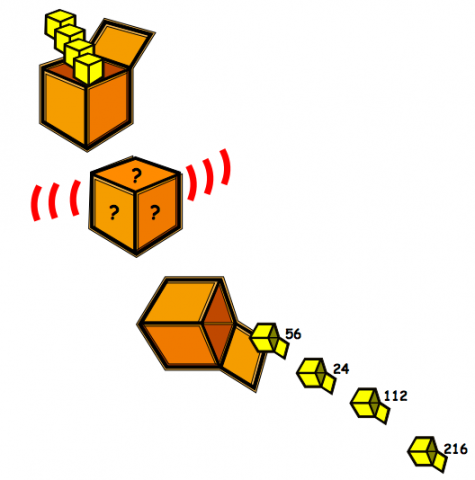
What's in the box?
This big box multiplies anything that goes inside it by the same number. If you know the numbers that come out, what multiplication might be going on in the box?
Problem
What's in the Box? printable sheet
In the picture below, four whole numbers are being put into the box. Inside the box, a multiplication happens to each number, and then four new numbers are tipped out of the box: 56, 24, 112 and 216.
What multiplication might have happened to each number inside the box to get the answers in the picture above?
Are there any other possibilities?
What's the largest number that each of the four starting numbers might have been multiplied by inside the box? How do you know?
-----------
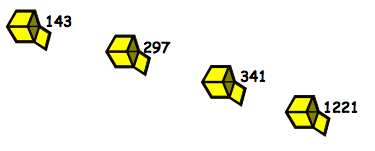
Imagine that four more numbers are put into the box, but now the box multiplies all of them by a new number. The numbers that come out of the box are:
143
297
341
1221
What number might the box be multiplying by? How do you know?
Discuss this with some other people and see if there are any different ways to work this out.
Getting Started
Remember, each of the four numbers that goes in is multiplied by the SAME number in the big box.
So, what is special about the four numbers that come out at the end?
Why don't you try out some ideas to see whether they work?
Student Solutions
We had a good number of solutions sent in with explanations as to how the answers were found. Ansh from Monkfield Park Primary School sent in the following:
For question 1) Answer is 8.
First of all I thought that 7 times 8 will be 56. Then I tried 3 times 8 and that also worked. Next I tried 13 times 8 that was 98 but that did not work so I tried 14 times 8 which was 112 and it was correct. Finally I divided 216 by 8 and ended up with 7.
So that's how I figured out that the multiplier is 8.
For question 2) Answer is 11
First of all I tried 3 and that did not work so I tried 6 and that did not work either. I also tried 7 and 9 but they both were wrong too. I knew it was not an even number so I skipped 2 and 10. Then I tried 11 and that worked.
So the first one was 13 times 11 = 143.
Next I divided 297 by 11 and the answer was 297.
After that I tried 341 divided by 11 and came up with 31.
Finally I did 1221 divided by 11 which gave me 111.
So the multiplier was 11.
Delaney at Mount Vernon School Maine, U.S. said:
Question 1 Possible factors: 2, 4 or 8
Largest common factor: 8
$56\div2=28$, $28\div2=14$, $14\div2=7$
$24\div2=12$, $12\div2=6$, $6\div2=3$
$112\div2=56$, $56\div2=28$, $28\div2=14$
$216\div2=108$, $108\div2=54$, $54\div2=27$
After I got these answers there were no more common factors and I assumed that 7, 3, 14, and 27 were the original numbers. 8 is the largest common factor because $2^3$ or 2x2x2=8.
Question 2 Only possible factor: 11
None of the numbers were even in this question so I knew that no multiples of two would be a common factor.
143=110+33
297=220+77
1221=1100+121
341=330+11
After dividing into portions divisible by 11, I found the original numbers by dividing by 11.
$143\div11=13$
$341\div11=31$
$1221\div11=111$
$297\div11=27$
There were no more common factors, so I assumed those were the original numbers.
We had this submitted from Jerry at Dulwich College, Shanghai:
First I checked which numbers that 143 can be divided by.
I skipped the multiples of 5 because 143, 297, 341 and 1221 clearly wouldn't be able to be divided by multiples of 5. I first found out 143 can be divided by 11 and 13. But 297 cannot be divided by 13. So I kept working on 11 and all four numbers can be divided by 11. So the winner is 11!
Well, altogether these have been very good responses to this challenge. Keep sending solutions to any other activity you have a go at.
Teachers' Resources
What's in the Box?
Four numbers in little boxes are put into a special big box that does a multiplication, then four new numbers come out at the end:
We only used whole numbers to go in, so, what multiplication might have gone on in the big box to get the answers in the picture above?
What was the largest number that could have been used to multiply by, in that big box?
Imagine four new boxes now (with new numbers in) and the large box multiplying by a different number this time. The numbers that come out are these:
What would be the number that the big box is multiplying by?
How are you working these out?
Discuss with others and see if there are different ways that you found the answers.
Why do this problem?
Of course this problem is rather like a function machine, but it can be more interesting for the pupils and easily extended to challenge a wide range of pupils. It could be used to introduce children to the idea of common factors and offers opportunities for learners to record in whatever way they choose.
Possible approach
It may be necessary to introduce the class to just one number going in and to give them one outcome to start with so that they understand the process. Then, gradually increase the number of numbers going in until you reach four, as in the problem. Your own examples can be adjusted in complexity according to the level of your pupils.
Once learners have had some time to work on the first part of the problem in pairs, ask them to share their ways of working with the whole group. Look out for those who give good reasons for choosing particular methods. At this stage, you could introduce the vocabulary of common factors if appropriate.
You may also wish to draw attention to interesting ways of recording. Some children may have drawn pictures, others may have written calculations and others may have done both.
Key questions
Possible extension
Pupils can be challenged to explain how they know they've found the largest possible number that the inputs have been multiplied by. Some pupils could go on to invent their own similar problems for others to do, including ones where a division is performed inside the box instead of a multiplication.
Possible support
Some pupils might benefit from beginning with the version of this task that uses addition and subtraction: What Was in the Box?
In order to introduce the multiplication version of this task, you can use sticks of cubes (such as multilink cubes) to represent one number going into the 'box'. Cover the cubes with a cloth and then secretly add the required extra number of cubes under the cover, in the form of more sticks of cubes, before revealing them to the child. Then a number of probing questions can be asked: How many cubes are there now? What has happened under the cover? Encourage pupils to consider how the number of sticks has grown, e.g. from 1 to 5, instead of simply counting how many more cubes there are.
As they tackle the main problem, some learners might find it useful to have a multiplication square or calculator available.