Can you draw a square in which the perimeter is numerically equal to the area?
Katie had a pack of 20 cards numbered from 1 to 20. She arranged the cards into 6 unequal piles where each pile added to the same total. What was the total and how could this be done?
Can you fill in this table square? The numbers 2 -12 were used to generate it with just one number used twice.
One quarter of these coins are heads but when I turn over two coins, one third are heads. How many coins are there?
The discs for this game are kept in a flat square box with a square hole for each. Use the information to find out how many discs of each colour there are in the box.
Mrs Morgan, the class's teacher, pinned numbers onto the backs of three children. Use the information to find out what the three numbers were.
This multiplication uses each of the digits 0 - 9 once and once only. Using the information given, can you replace the stars in the calculation with figures?
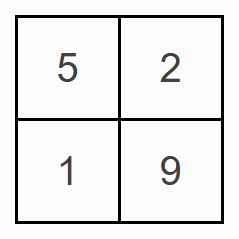
Choose four different digits from 1-9 and put one in each box so that the resulting four two-digit numbers add to a total of 100.
Can you make square numbers by adding two prime numbers together?
Can you make a cycle of pairs that add to make a square number using all the numbers in the box below, once and once only?
