Cubes and cuboids

Imagine a 4 by 4 by 4 cube. If you and a friend drill holes in some of the small cubes in the ways described, how many will not have holes drilled through them?

A useful visualising exercise which offers opportunities for discussion and generalising, and which could be used for thinking about the formulae needed for generating the results on a spreadsheet.

This problem is about investigating whether it is possible to start at one vertex of a platonic solid and visit every other vertex once only returning to the vertex you started at.

Nicola has lost a piece of her 3D jigsaw. Can you work out the shape of the missing piece?

According to Plutarch, the Greeks found all the rectangles with integer sides, whose areas are equal to their perimeters. Can you find them? What rectangular boxes, with integer sides, have their surface areas equal to their volumes?

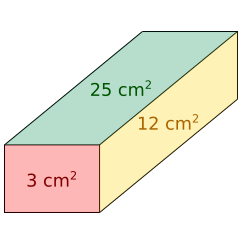
A box has faces with areas 3, 12 and 25 square centimetres. What is the volume of the box?

A 3×3×3 cube may be reduced to unit cubes in six saw cuts. If after every cut you can rearrange the pieces before cutting straight through, can you do it in fewer?

Toni Beardon has chosen this article introducing a rich area for practical exploration and discovery in 3D geometry