Wrapping Gifts
A box of size a cm by b cm by c cm is to be wrapped with a square piece of wrapping paper. Without cutting the paper what is the smallest square this can be?
Problem
Image

A box of size $a$ cm by $b$ cm by $c$ cm is to be wrapped with a square shaped piece of wrapping paper. Cutting the paper is not allowed so what is the smallest square this sheet can be?
Now suppose we want to wrap up a cube, what is the smallest square of wrapping paper that can be used to minimise wastage?
Student Solutions
The solution here comes from Tom, Ella and James of Madras College,
St Andrews, Scotland. They prove that, to use the smallest square
of wrapping paper to wrap a cuboid shape, you should place the
cuboid symmetrically with its longest edges parallel to the
diagonal of the wrapping paper and with a face containing the two
longest edges on the paper. If $c$ is the longest edge of the
cuboid, $b$ is the middle one and $a$ is the shortest edge of the
cuboid then the length of the diagonal of the wrapping paper has to
be at least $2c + 2a$ so the square has to be $(c + a)\sqrt 2$ by
$(c + a)\sqrt 2$. In this case the edges of the wrapping paper will
only just meet.
The smallest square of wrapping paper to wrap a cube of edge length $a$ is a square of side $2a\sqrt 2$.
Here is Tom, Ella and James' solution:
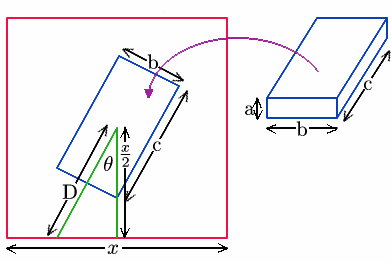
Let the square of wrapping paper be $x$ units by $x$ units. Using simple trigonometry $D \cos \theta = x / 2$. To make the edges of the paper meet, $D$ must have a length $c / 2$ to go under the cuboid, $a$ to go up the side and another $c / 2$ to go over the top. $$D = c / 2 + a + c / 2 = c + a$$ $$x = 2(c + a ) \cos \theta$$ Looking at this it is simply a scaling of the cosine graph.
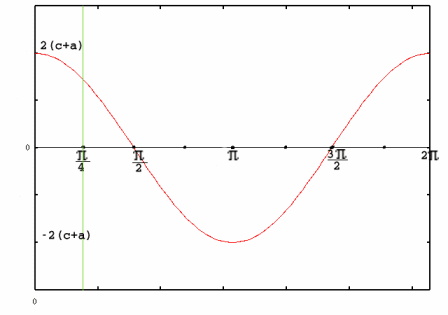
Because of the symmetries involved we are only considering $0 \leq \theta \leq \pi/4$. In this interval the cosine graph is always stationary or decreasing so $\theta = \pi/4$ gives the minimum value.
The smallest wrapping paper therefore has sides of length $$x = 2(c + a)\cos \pi/4 = \sqrt 2 (c + a)$$ where $c$ is the length of longest edge of the cuboid and $a$ is the length of the shortest edge.
Using this formula for a cube of side $a$ the wrapping paper to minimize wastage is a square of size $2\sqrt 2 a$. The area of the paper is $8a^2$ so the area of paper not actually used to cover the cube is $2a^2$. If the cube is placed centrally on the wrapping paper with edges parallel to the diagonals of the paper, when wrapping the cube the edges of the paper will just meet at the top of the cube and the 'wastage' will be a triangle of area $a^2/2$ at each corner.
The smallest square of wrapping paper to wrap a cube of edge length $a$ is a square of side $2a\sqrt 2$.
Here is Tom, Ella and James' solution:
Image

Let the square of wrapping paper be $x$ units by $x$ units. Using simple trigonometry $D \cos \theta = x / 2$. To make the edges of the paper meet, $D$ must have a length $c / 2$ to go under the cuboid, $a$ to go up the side and another $c / 2$ to go over the top. $$D = c / 2 + a + c / 2 = c + a$$ $$x = 2(c + a ) \cos \theta$$ Looking at this it is simply a scaling of the cosine graph.
Image

Because of the symmetries involved we are only considering $0 \leq \theta \leq \pi/4$. In this interval the cosine graph is always stationary or decreasing so $\theta = \pi/4$ gives the minimum value.
The smallest wrapping paper therefore has sides of length $$x = 2(c + a)\cos \pi/4 = \sqrt 2 (c + a)$$ where $c$ is the length of longest edge of the cuboid and $a$ is the length of the shortest edge.
Using this formula for a cube of side $a$ the wrapping paper to minimize wastage is a square of size $2\sqrt 2 a$. The area of the paper is $8a^2$ so the area of paper not actually used to cover the cube is $2a^2$. If the cube is placed centrally on the wrapping paper with edges parallel to the diagonals of the paper, when wrapping the cube the edges of the paper will just meet at the top of the cube and the 'wastage' will be a triangle of area $a^2/2$ at each corner.
