Cubes
Problem
In this activity we will be using cubes to make different arrangements. First, find three cubes that are all the same size and all have flat faces.

Start by looking at just one of these cubes.

Put it onto the table or another flat surface. How many square faces can you see? You are allowed to walk around the cube and bend down to see it, but you aren't allowed to pick the cube up. Click on the button below to check your answer:
There are five faces that we can see, because the sixth face is against the table.
Next, take two of the cubes. Put them down on the table, either separately or together. What different arrangements are there?
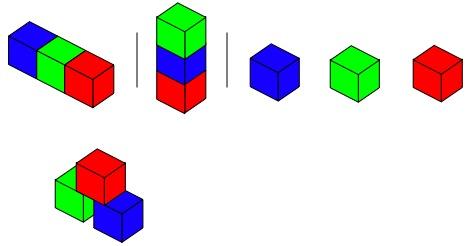
I've made these three arrangements with my cubes:

How many square faces can I see in each case? Have a go at using your imagination to visualise how many I can see, and try making these arrangements yourself to check your answers. Then click on the button below:
In the second example, I can see eight faces - one at each end, then three lots of two faces.
In the third example, I can see ten faces - there are two lots of five faces.
These three arrangements each showed me a different number of faces. Are there any other ways in which I could have arranged the cubes? Would these show me a different number of faces?
Think about how we can tell whether or not two arrangements are the same. For example, I could turn the second arrangement so that the red cube is pointing to the left instead - would this count as a different arrangement? Why/why not?
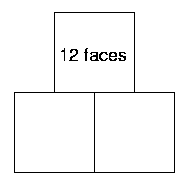
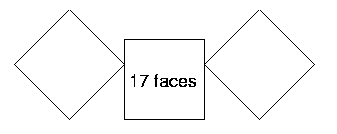
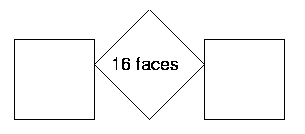
Finally, take all three of the cubes. Arrange these in some different ways. It might help to write or draw each arrangement to keep track of the ways that you have already tried. Here are some of my arrangements:

How many square faces can I see in each of these three cases?
Now it's your turn! Use your three cubes every time, and see how many different ways there are to arrange them. How many faces can you see each time? Try to find all the possible answers.
Further challenge:
What happens if the faces don't line up completely? Look at the example below:

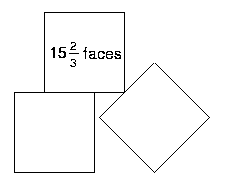
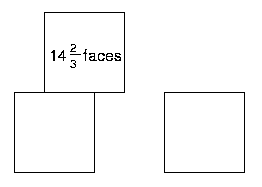
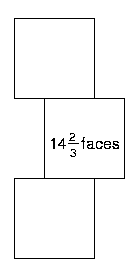
$5\frac{1}{3}$ + $4\frac{2}{3}$ + $4\frac{2}{3}$ = $14\frac{2}{3}$
How many arrangements can you find where the faces don't line up completely? How many different ways of doing this do you think there are?
Getting Started
You'll find this investigation easier if you have some cubes to make your arrangements with.
If you have plenty of cubes, you could keep each arrangement to compare it to the others, rather than breaking it up. You could also take photos of your different arrangements if you're finding it difficult to draw them or record them in another way.
Student Solutions
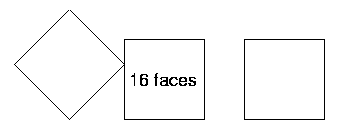
Friar's Grove Junior School sent in lots of solutions. These are some of them. How clever to think of balancing a cube on an edge! Look closely at the ones using thirds of faces. Do you get the same results?
Image
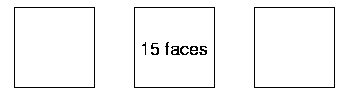
|
|
Image
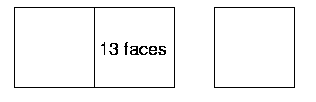
Image
|
|
Image
Image
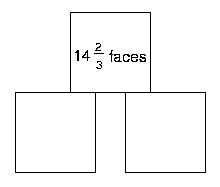
|
|
Image
Image
|
|
Image
Image
|
|
|
Image
Image
|
Teachers' Resources
Why do this problem?
Possible approach
If, as the adult, you need to see in advance what ideas may, and I emphasise may, come from the pupils then click here.

Key questions
Possible extension
For more extension work