Four points on a cube
Problem
Take a cube of side length one unit. A vertex of the cube and the centres of the three faces not containing that vertex form the vertices of a tetrahedron. What is the surface area of this tetrahedron?
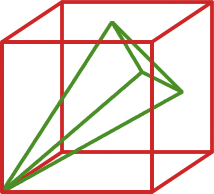
Getting Started
Student Solutions
Congratulations to Ang Zhi Ping from River Valley High School, Singapore for this solution.
Take the vertex of the cube at the origin $(0,0,0)$ as shown in the diagram. The tetrahedron has vertices $O,X,Y,Z$, where the three centres $X$, $Y$ and $Z$ are as follows: $$ X=\left(1,\frac{1}{2},\frac{1}{2}\right), Y=\left(\frac{1}{2},1,\frac{1}{2}\right), Z=\left(\frac{1}{2},\frac{1}{2},1\right). $$
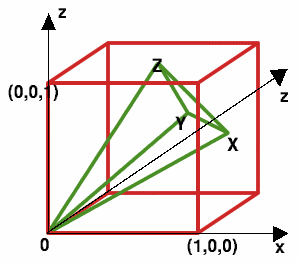
The area required is the sum of the areas of the triangles $XYZ$ (which is equilateral), and $OXY$, $OYZ$, $OZX$ (which are congruent to each other and isosceles).
Now $XY= 1/\sqrt{2}$ so that $$ area(XYZ) = \frac{1}{2} \left(\frac{1}{\sqrt{2}}\right)^2 \sin 60^\circ = \frac{\sqrt{3}}{8} $$ Next, $$ OX = OY = OZ = \sqrt{\frac{3}{2}}. $$ Thus $$ OX = OY = \sqrt{\frac{3}{2}}, XY = \frac{1}{\sqrt{2}}. $$ This gives the area of $OXY$ as $\sqrt{11}/8$. Thus the surface area of the tetrahedron is $$ \frac{\sqrt{3}}{8} + \frac{3\sqrt{11}}{8}. $$
Teachers' Resources
It gives experience of using 3D coordinates, visualisation, and using the distance formula in 3D, and formulae for the area of a triangle.
Possible approach
A good diagram isessential. You might discuss and draw and label the diagram as a class effort and then the students could complete the calculatons independently.
Key questions
What are the coordinates of the vertices of the tetrahedron?
