2D shapes and their properties
-

-
 problem
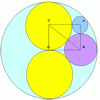
problemRetracircles
Four circles all touch each other and a circumscribing circle. Find the ratios of the radii and prove that joining 3 centres gives a 3-4-5 triangle. -
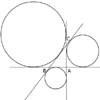 problem
problemEscriptions
For any right-angled triangle find the radii of the three escribed circles touching the sides of the triangle externally. -
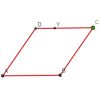 problem
problemRoaming Rhombus
We have four rods of equal lengths hinged at their endpoints to form a rhombus ABCD. Keeping AB fixed we allow CD to take all possible positions in the plane. What is the locus (or path) of the point D? -
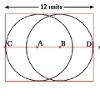 problem
problemNot so Little X
Two circles are enclosed by a rectangle 12 units by x units. The distance between the centres of the two circles is x/3 units. How big is x? -
 problemFavourite
problemFavouriteHex
Explain how the thirteen pieces making up the regular hexagon shown in the diagram can be re-assembled to form three smaller regular hexagons congruent to each other. -
 problem
problemCircles in Circles
This pattern of six circles contains three unit circles. Work out the radii of the other three circles and the relationship between them. -
 problem
problemOverlapping Circles
What shaped overlaps can you make with two circles which are the same size?
-
 problem
problemPentagonal
Can you prove that the sum of the distances of any point inside a square from its sides is always equal (half the perimeter)? Can you prove it to be true for a rectangle or a hexagon? -
 problem
problemCentral Distance
Weekly Problem 1 - 2006
The diagram shows two circles enclosed in a rectangle. What is the distance between the centres of the circles?
